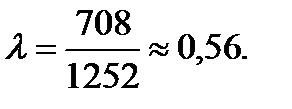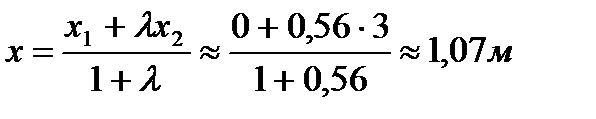Властивості проекцій
1. 2. 3. 4. Доведемо 2. 1). 2).
2.7 Декартові координати вектора та точки Розглянемо прямокутну систему координат в просторі
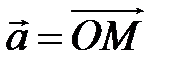 . Через кінець вектора . Через кінець вектора 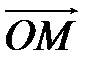 проведемо площини, паралельні координатним площинам, отримаємо паралелепіпед, однією із діагоналей якого є проведемо площини, паралельні координатним площинам, отримаємо паралелепіпед, однією із діагоналей якого є 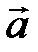 (рис.2.10). (рис.2.10).
За означенням суми декількох векторів маємо: Рисунок 2.10 Вектори
Нехай точка Напрямні косинуси Нехай дано
Таким чином, будь-якийвектор має орт:
2.8 Ділення відрізка в даному відношенні
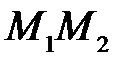 (рис.2.11) в даному відношенні (рис.2.11) в даному відношенні 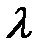 >0 означає на даному відрізку знайти таку точку >0 означає на даному відрізку знайти таку точку 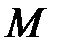 , для якої виконується рівність: , для якої виконується рівність:
Рисунок 2.11 Нехай є т.
Тоді
Таким чином: Якщо т.
Приклад 1. Горизонтальна балка довжиною 3 м і масою 80 кг вільно лежить своїми кінцями на двох рухомих опорах
Рисунок 2.12 Розв'язання. Маса балки 80 кг складає 784 Н. На опору діє половина ваги балки. Тобто 392 Н. Вага масою 200 кг діє на балку силою 1960 Н. На частину опори Прийнявши точку А за початок координат (рис. 2.12), ділимо відрізок у відношенні Тоді: Таким чином, щоб тиск на опору
|

 , якщо
, якщо  , або
, або  .
. .
. .
. .
.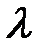 > 0
> 0  .
. .
. . На кожній осі виберемо одиничний вектор, напрям якого співпадає з додатнім напрямком осей
. На кожній осі виберемо одиничний вектор, напрям якого співпадає з додатнім напрямком осей  ,
,  ,
,  ,
,  . Ці три взаємно перпендикулярні вектори називаються ортами. Так як вони некомпланарні, то вони утворюють базис, який називається декартовим ортогональним базисом.
. Ці три взаємно перпендикулярні вектори називаються ортами. Так як вони некомпланарні, то вони утворюють базис, який називається декартовим ортогональним базисом.








 , але
, але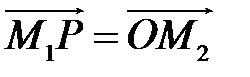 ,
, 

 .
. ,
,  ,
,  є складовими векторами
є складовими векторами  по осям
по осям 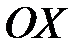 ,
,  ,
,  , але
, але  ,
,  ,
,  .
.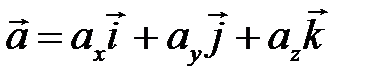
 має координати
має координати  . Напрямлений відрізок
. Напрямлений відрізок  називається радіус-вектором т.
називається радіус-вектором т.  , тоді проекції вектора
, тоді проекції вектора  ,
,  ,
,  і
і  – декартові координати
– декартові координати 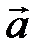 .
. , тоді:
, тоді: ;
; ;
; .
.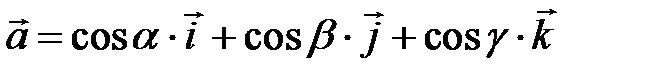 .
.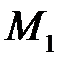


 , або
, або 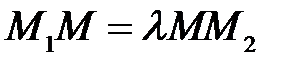 . (2.1)
. (2.1) і т.
і т.  . Знайдемо координати точки
. Знайдемо координати точки  . Оскільки виконується рівність (2.1), маємо:
. Оскільки виконується рівність (2.1), маємо: .
. ;
; ;
; .
. ,
,  ,
,  .
. середина відрізка
середина відрізка  , тобто
, тобто  , то:
, то: ,
,  ,
, 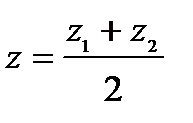 .
. і
і 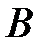 (рис.2.12). На відстані від кінця
(рис.2.12). На відстані від кінця