Гіпербола
Означення 6. Крива другого порядку (3.16)називається гіперболою, якщо коефіцієнт

 (3.21) (3.21)
Якщо Точки Рисунок 3.15 є ексцентриситетом гіперболи. Характеристична властивість гіперболи Теорема 2. Для будь-якої точки гіперболи абсолютна величина різниці її фокальних радіусів, величина стала і дорівнює Гіпербола має асимптоти Парабола

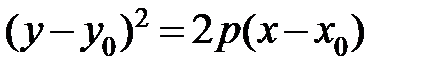 (3.22) називається параболою з вершиною (3.22) називається параболою з вершиною 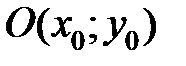 і параметром і параметром 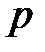 . Пряма . Пряма  – вісь симетрії параболи. – вісь симетрії параболи.
Для Точка
Рисунок 3.16 Характеристична властивість параболи Теорема 3. Відстань від довільної точки параболи до фокуса дорівнює відстані до директриси, тобто Полярна система координат Візьмемо на площині т.
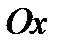 – полярну вісь, тоді довільна точка площини матиме координати – полярну вісь, тоді довільна точка площини матиме координати  , де , де 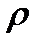 – полярний радіус, що з’єднує полюс з точкою, а – полярний радіус, що з’єднує полюс з точкою, а  – полярний кут (рис.3.17). – полярний кут (рис.3.17).
Рисунок 3.17 Зауваження. Кожній парі чисел Наприклад Зв'язок між прямокутними і полярними координатами: Обернений зв'язок:
|

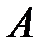 і
і  рівняння (3.16) мають різні знаки, тобто
рівняння (3.16) мають різні знаки, тобто 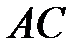 <
<  :
: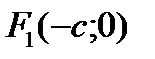
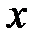
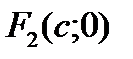
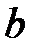

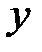
 , то
, то 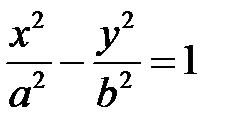 (рис.3.15).
(рис.3.15).
 , де
, де  , є фокусами гіперболи.
, є фокусами гіперболи. 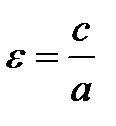 , де
, де 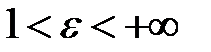
 :
: 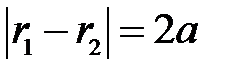 .
.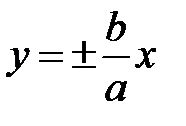 .
.
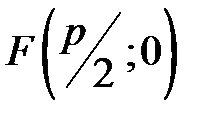
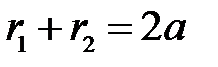 0
0
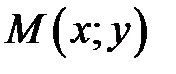
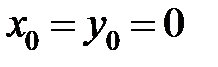 маємо
маємо 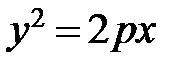 (рис.3.16).
(рис.3.16).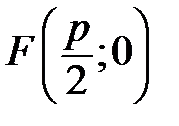 – фокус параболи, а
– фокус параболи, а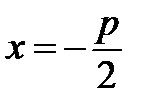 – директриса параболи.
– директриса параболи.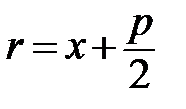 .
. , яку назвемо полюсом. Проведемо з
, яку назвемо полюсом. Проведемо з 


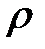
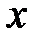

 ,
, 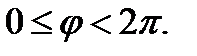
 , якщо проти руху годинникової стрілки.
, якщо проти руху годинникової стрілки.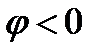 , якщо за годинниковою стрілкою.
, якщо за годинниковою стрілкою.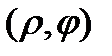 відповідає єдина точка площини, але кожній точці площини – не єдина пара чисел.
відповідає єдина точка площини, але кожній точці площини – не єдина пара чисел.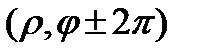 відповідає одна і та ж точка.
відповідає одна і та ж точка.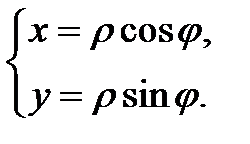
 ,
, 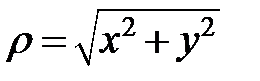 ,
,  ,
, 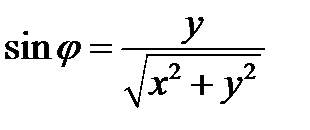 .
.


