Властивості числових послідовностей
1. Якщо послідовність збіжна,то вона обмежена. Доведення. Нехай
Нехай 2. Будь-яка збіжна послідовність має тільки одну границю. Доведення. Використаємо метод від протилежного. Нехай послідовність
Так як всі елементи послідовності 3. Якщо 4. Якщо змінні 5. Якщо
Доведення. Нехай Тоді: Що і потрібно було довести. 6. Якщо
7. Якщо
Теорема. (Ознака збіжності послідовності) Доведемо, що Доведення. Розглянемо послідовність Доведемо, що вона збіжна. Для цього необхідно довести, що вона зростає та обмежена зверху. За формулою Бінома-Ньютона:
де
При За формулою суми геометричної прогресії Так, змінна величина
|

 – збіжна і
– збіжна і 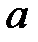 – її границя. Візьмемо ε > 0,
– її границя. Візьмемо ε > 0,  – номер починаючи з якого
– номер починаючи з якого 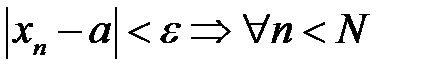

 :
: 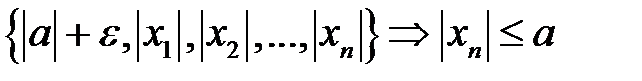 для
для  – обмежена.
– обмежена. границі
границі  і
і 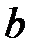 . Тоді
. Тоді  і
і  .
.
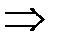

 мають одне і теж стале значення
мають одне і теж стале значення  , то
, то 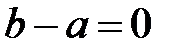
 а це суперечить нашому припущенню.
а це суперечить нашому припущенню. і
і  то
то 
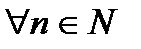 .
.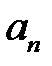 і
і  – збігаються до однієї границі, то змінна
– збігаються до однієї границі, то змінна  , така що
, така що  , також збігається до цієї границі.
, також збігається до цієї границі. ,
,  збіжні, то
збіжні, то 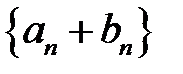 також збіжна і границя
також збіжна і границя
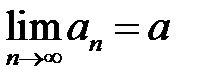 ,
,  Тоді задамо
Тоді задамо 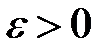 і візьмемо
і візьмемо  таке, що
таке, що 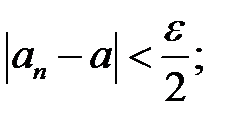

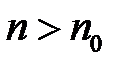 .
. .
.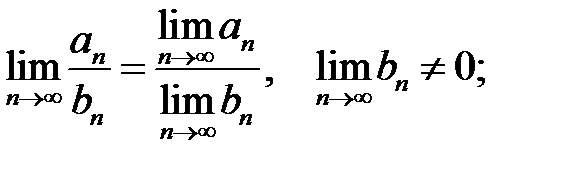
 .
.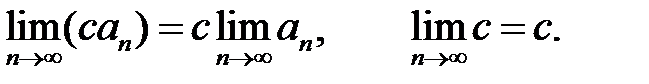
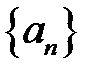 монотонно зростає (спадає) і обмежена зверху (знизу), то вона має границю:
монотонно зростає (спадає) і обмежена зверху (знизу), то вона має границю: 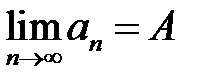 ,
, 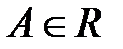 .
.



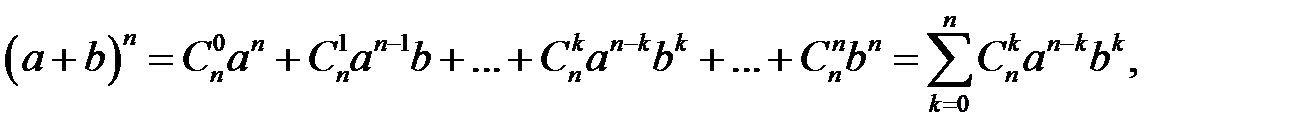
 – число сполучень,
– число сполучень, 

 і
і 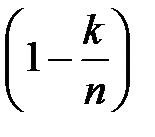 <
< 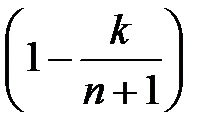 коли 0<
коли 0<  <
< 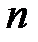
 <
<  – зростаюча. Також бачимо, що:
– зростаюча. Також бачимо, що: 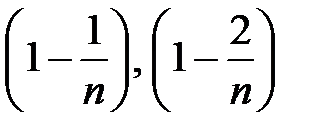 і т.д. в розкладі
і т.д. в розкладі 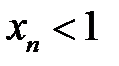 , а
, а 
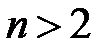

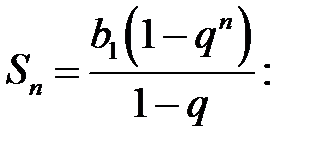
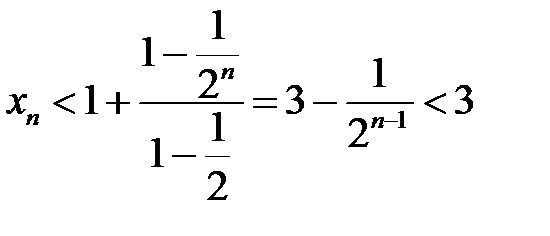 – обмежена зверху.
– обмежена зверху. – зростаюча і обмежена, тому за ознакою збіжності послідовності вона має границю. Ця границя позначається літерою
– зростаюча і обмежена, тому за ознакою збіжності послідовності вона має границю. Ця границя позначається літерою 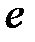 :
: 


