Похідна функції
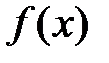 (рис.4.28). Розглянемо два значення аргументу (рис.4.28). Розглянемо два значення аргументу 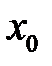 і і 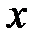 : :
Рисунок 4.28 Означення 1. Похідною Нехай на кривій задана т. Означення 2. Дотичною є пряма, яка займає граничне положення січної. Розглянемо графік функції
Рисунок 4.29 Висновок. Кутовий коефіцієнт дотичної до графіка функції в точці з абсцисою
Означення 3. Якщо функція Означення 4. Функція Зауваження. Знаходження похідної функції називають диференцію-ванням. Якщо функція диференційовна в кожній точці деякого відрізка Теорема. Якщо функція диференційовна в будь якій точці, то вона неперервна в ній. З теореми випливає, що в точках розриву функція не має похідної. Проте обернене твердження неправильне. Тобто, з того, що в деякій точці функція неперервна ще не випливає, що в цій точці вона диференційовна.
|




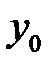

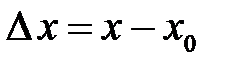
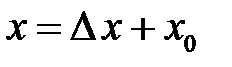
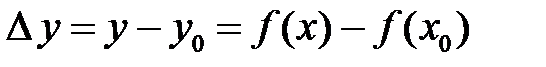
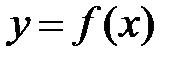 в т.
в т. 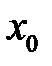 називається границя відношення приросту функції
називається границя відношення приросту функції 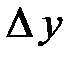 в цій точці, до приросту аргументу
в цій точці, до приросту аргументу  , якщо
, якщо  :
: 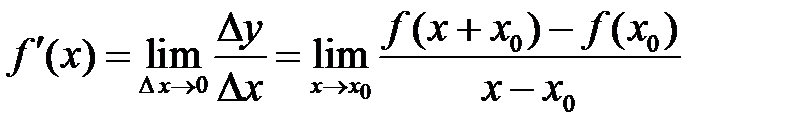
 .
. невертикальну дотичну
невертикальну дотичну  (рис.4.29). Знайдемо кутовий коефіцієнт
(рис.4.29). Знайдемо кутовий коефіцієнт 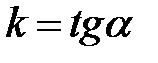 , для цього проведемо через т.
, для цього проведемо через т. 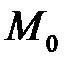 січну
січну 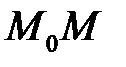 де
де 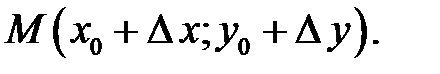 Її кутовий коефіцієнт
Її кутовий коефіцієнт  , при
, при  ,
,  при цьому січна
при цьому січна  необмежено наближається до дотичної
необмежено наближається до дотичної  , а тому
, а тому  – кутовий коефіцієнт дотичної:
– кутовий коефіцієнт дотичної: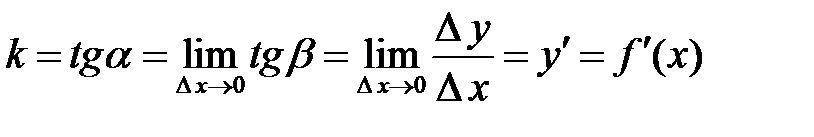



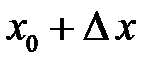







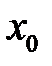 дорівнює значенню похідної цієї функції в т.
дорівнює значенню похідної цієї функції в т.  :
: .
.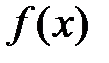 має неперервну похідну
має неперервну похідну  на
на  , то функція
, то функція  називається гладкою на цьому проміжку.
називається гладкою на цьому проміжку. похідна якої
похідна якої  допускає тільки скінчене число точок розриву, причому I-го роду, на даному проміжку
допускає тільки скінчене число точок розриву, причому I-го роду, на даному проміжку  , називається кусково-гладкою на цьомупроміжку.
, називається кусково-гладкою на цьомупроміжку. чи на інтервалі
чи на інтервалі  , то кажуть, що вона диференційовна відповідно на відрізу чи на інтервалі.
, то кажуть, що вона диференційовна відповідно на відрізу чи на інтервалі.


