Похідні вищих порядків
Означення 1. Якщо функція має першу похідну, то похідна від похідної першого порядку називається похідною другого порядку або другою похідною:
аналогічно: Похідна позначається римськими цифрами: Фізичний зміст похідної другого порядку – Друга похідна функції заданої параметрично знаходиться за формулою:
Поняття диференціала Якщо функція Відповідно до теореми про зв'язок границі функції і нескінченно малої можна записати: Означення 1. Якщо функція Так як Формули і властивості похідної, справедливі і для диференціала. Геометричний зміст диференціала. Нехай дано функцію Зауваження:
Рисунок 4.31 Застосування диференціала до наближених обчислень
Означення 2. Абсолютною похибкою Означення 3. Відносною похибкою
|

 ;
; .
. або
або 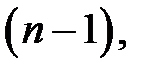
 .
. − прискорення прямолінійного руху за час
− прискорення прямолінійного руху за час  .
. .
. диференційовна на
диференційовна на  , то
, то  .
. , де
, де  , коли
, коли  , тоді
, тоді  .
.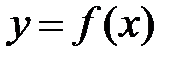 має в точці
має в точці  похідну
похідну  , тоді добуток
, тоді добуток  називається диференціалом функції
називається диференціалом функції 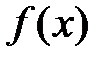 в т.
в т. 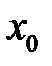 . Записують
. Записують  .
. тобто
тобто  маємо
маємо  .
. – дотична (рис.4.31). З
– дотична (рис.4.31). З  маємо
маємо  . Але
. Але  ,
,  .
.  . Таким чином диференціал функції
. Таким чином диференціал функції 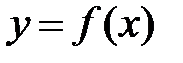 в т.
в т.  дорівнює приросту ординати дотичної.
дорівнює приросту ординати дотичної.
 , але при малих
, але при малих  ,
,  .
.



 – формула наближеного обчислення значення функції.
– формула наближеного обчислення значення функції. наближеної величини
наближеної величини  називається модуль різниці між її точним значенням
називається модуль різниці між її точним значенням  та наближеним:
та наближеним:  .
. називають:
називають:  .
.


