Границя та неперервність функції багатьох змінних
Означення 1. Функція, залежна від двох та більше змінних, називається функцією багатьох змінних (ФБЗ) Означення 2. Областю визначення ФБЗ є множина точок Приклад 1. Знайти область визначення функції
Відповідь: рис.5.1. Рисунок 5.1 Приклад 2. Знайти область визначення функції Розв’язання.
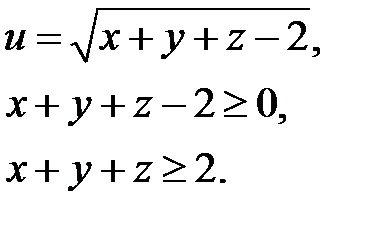
Відповідь: рис.5.2.
Рисунок 5.2 Означення 3. Лінією рівня функції Приклад 3. Побудувати лінії рівня функцій
Відповідь: рис.5.3.
Рисунок 5.3 Означення 4. Поверхнею рівня функції Приклад 4. Побудувати поверхні рівня
Відповідь: рис.5.4.
Рисунок 5.4
 є множина
усіх точок нерівності
Рисунок 5.5 Означення 6. Число
Означення 7. Функція Означення 8. Функція Зауваження. Усі теореми і властивості однієї змінної справедливі для функції багатьох змінних.
|
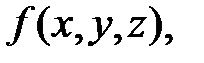
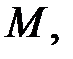для яких функція 
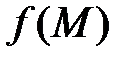визначена.
.
.
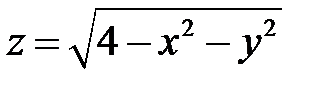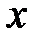
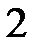
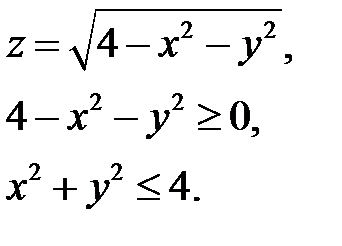
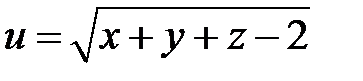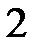
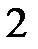
називається лінія 
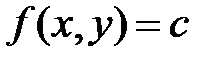, в площині 
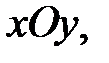в точках якої функція зберігає стале значення 
.
.
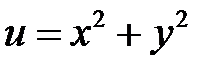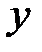
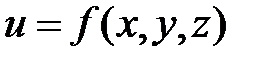називається поверхня 
, в точках якої функція зберігає стале значення 
.
.
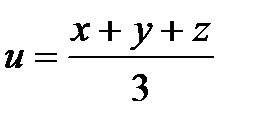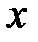
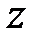
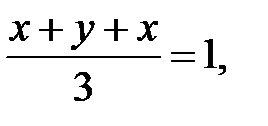
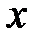
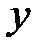
, які задовольняють
. 
– окіл (рис.5.5).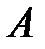
називається границею функції 
коли 
, якщо для будь-якої послідовності точок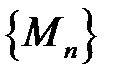 
таких, що 
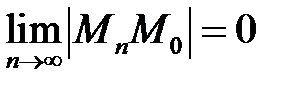, виконується рівність: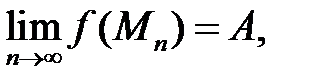
.
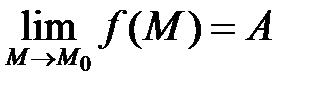називається неперервною в точці 
, якщо виконується рівність 
. У випадку двох змінних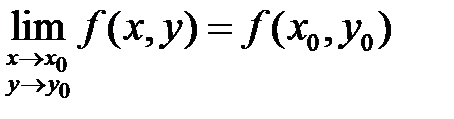 
.
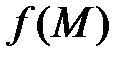називається неперервною на множині, якщо вона неперервна в будь-якій точці цієї множини.
