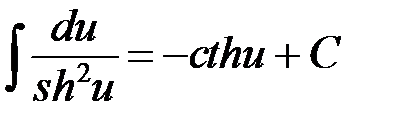Означення 1. Функція  називається первісною для даної функції
називається первісною для даної функції 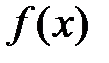 на проміжку
на проміжку 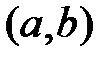 , якщо
, якщо  для будь-яких
для будь-яких 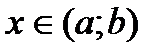 .
.
Теорема 1. Якщо  і
і 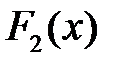 – дві первісні для функції
– дві первісні для функції 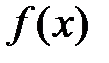 на проміжку
на проміжку 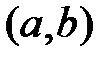 , то їх різниця дорівнює сталому числу.
, то їх різниця дорівнює сталому числу.
Доведення.
Нехай 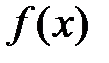 існує на проміжку
існує на проміжку 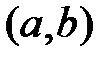 , та
, та  і
і 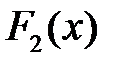 її первісні. За означенням 1 маємо
її первісні. За означенням 1 маємо 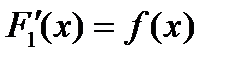 та
та 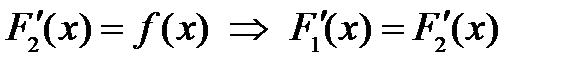 .
.
За наслідком з теореми Лагранжа, маємо 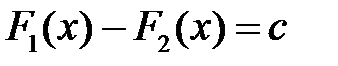 , де
, де 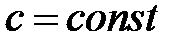 , тобто,
, тобто, 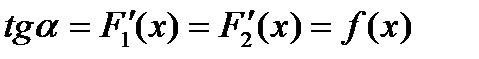 . Теорему доведено.
. Теорему доведено.
Наслідок. Якщо  первісна для деякої функції
первісна для деякої функції 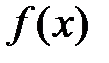 , то будь-яка інша первісна для
, то будь-яка інша первісна для 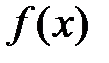 має вигляд
має вигляд 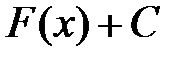 .
.
Означення 2. Невизначеним інтегралом від функції 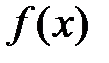 називається сукупність всіх первісних для функції
називається сукупність всіх первісних для функції 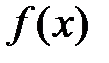 і позначається символом
і позначається символом 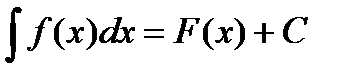 , де
, де 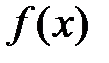 – підінтегральна функція,
– підінтегральна функція, 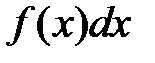 – підінтегральний вираз,
– підінтегральний вираз, 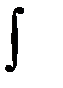 – знак інтеграла.
– знак інтеграла.
Інтегруванням називається операція знаходження первісної для даної функції 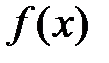 . Крива
. Крива  називається інтегральною кривою.
називається інтегральною кривою.
Властивості невизначеного інтеграла
1. 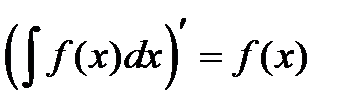
2. 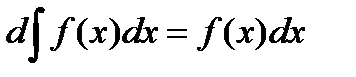
3. 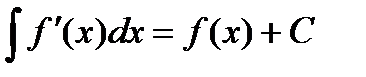
4. 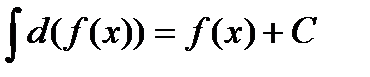
5. 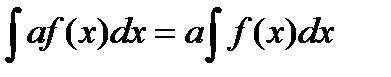 , де
, де 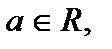
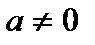
6. 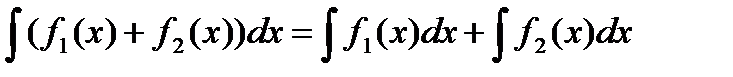
Знаки 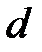 i
i 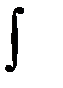 слідуючи один за одним в будь-якій послідовності взаємознищуються.
слідуючи один за одним в будь-якій послідовності взаємознищуються.
Доведемо 5-ту властивість:
Нехай  – первісна
– первісна 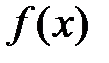 .
.
За означенням 2 маємо: 
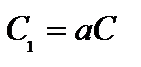 .
.
Тоді 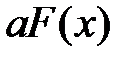 є первісною для функції
є первісною для функції 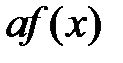 . Дійсно, за означенням 1:
. Дійсно, за означенням 1:
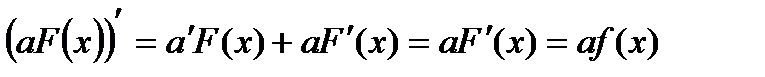 .
.
Таблиця невизначених інтегралів
Нехай 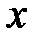 – незалежна змінна, функція
– незалежна змінна, функція 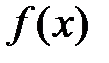 неперервна на даному інтервалі і
неперервна на даному інтервалі і  – її первісна.
– її первісна.
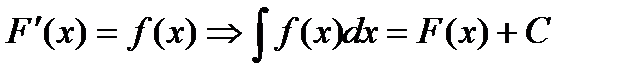 (6.1)
(6.1)
Нехай 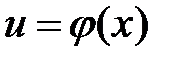 , де
, де 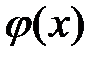 неперервна і диференційовна, а
неперервна і диференційовна, а 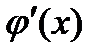 неперервна. Розглянемо
неперервна. Розглянемо 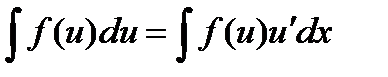 . (6.2)
. (6.2)
В даному випадку складена функція 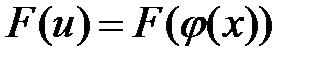 є первісною для підінтегральної функції (6.2). Тоді знайдемо
є первісною для підінтегральної функції (6.2). Тоді знайдемо
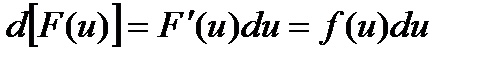
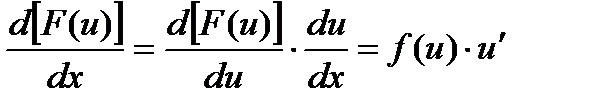 .
.
Це означає 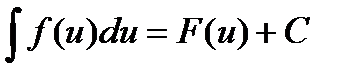 , (6.3)
, (6.3)
де 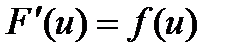 .
.
Тобто, мають місце (6.1) і (6.3).
Зауваження. Деякі перетворення диференціалів  :
:
1. 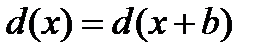 , де
, де 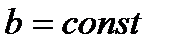 .
.
2. 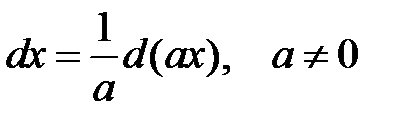 .
.
3. 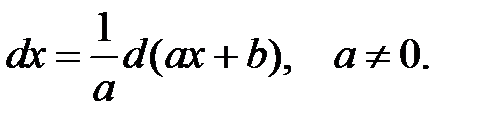
4. 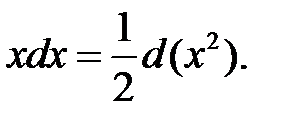
5. 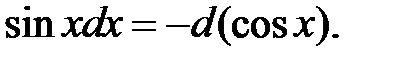
6. 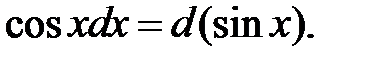
Таблиця інтегралів
1.  10.
10. 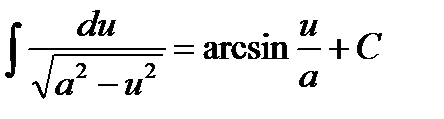
2. 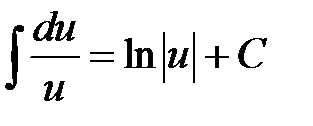 11.
11. 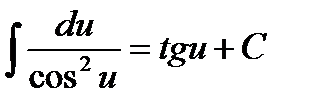
3.  12.
12. 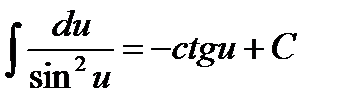
4. 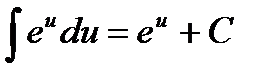 13.
13. 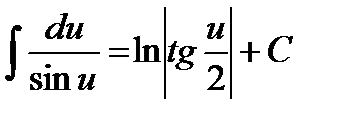
5.  14.
14. 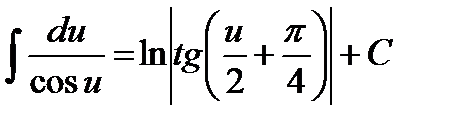
6. 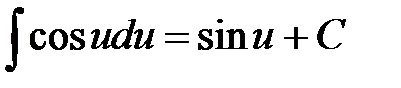 15.
15. 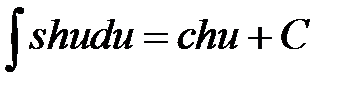
7. 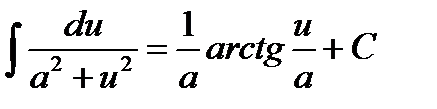 16.
16. 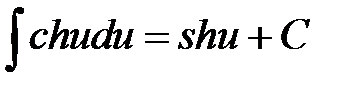
8. 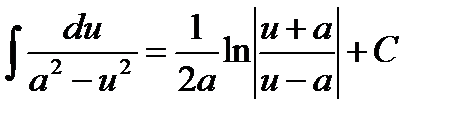 17.
17. 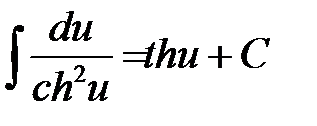
9.  18.
18. 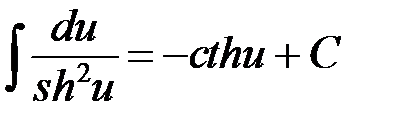

 називається первісною для даної функції
називається первісною для даної функції 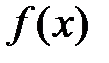 на проміжку
на проміжку 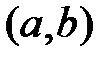 , якщо
, якщо  для будь-яких
для будь-яких 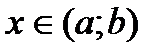 .
. і
і 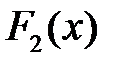 – дві первісні для функції
– дві первісні для функції 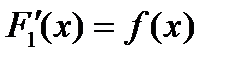 та
та 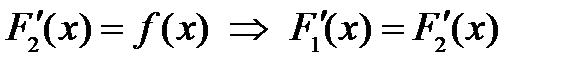 .
.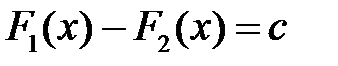 , де
, де 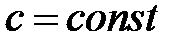 , тобто,
, тобто, 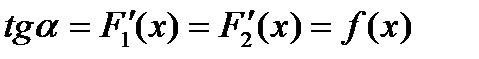 . Теорему доведено.
. Теорему доведено.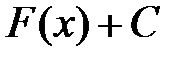 .
.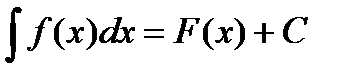 , де
, де 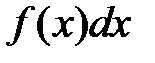 – підінтегральний вираз,
– підінтегральний вираз, 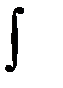 – знак інтеграла.
– знак інтеграла.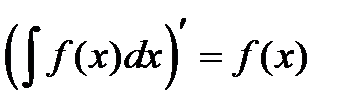
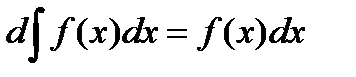
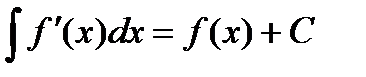
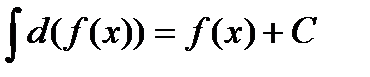
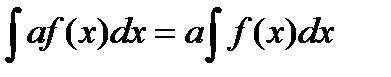 , де
, де 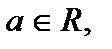
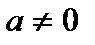
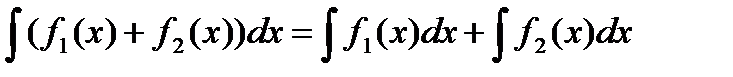
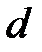 i
i 
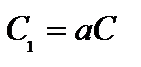 .
.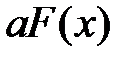 є первісною для функції
є первісною для функції 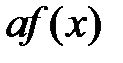 . Дійсно, за означенням 1:
. Дійсно, за означенням 1: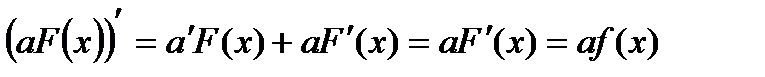 .
.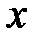 – незалежна змінна, функція
– незалежна змінна, функція 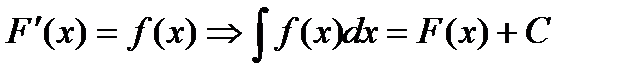 (6.1)
(6.1)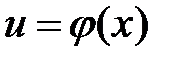 , де
, де 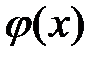 неперервна і диференційовна, а
неперервна і диференційовна, а 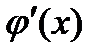 неперервна. Розглянемо
неперервна. Розглянемо 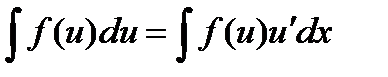 . (6.2)
. (6.2)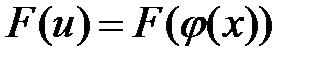 є первісною для підінтегральної функції (6.2). Тоді знайдемо
є первісною для підінтегральної функції (6.2). Тоді знайдемо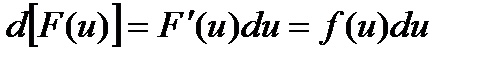
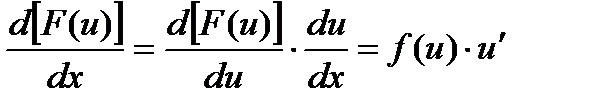 .
.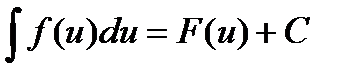 , (6.3)
, (6.3)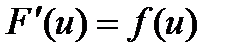 .
. :
: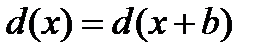 , де
, де 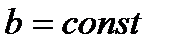 .
.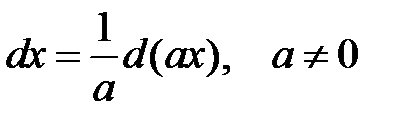 .
.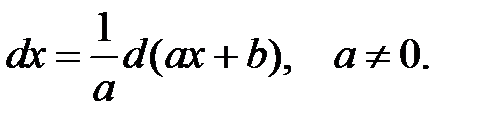
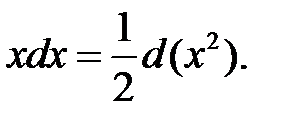
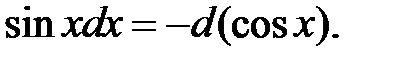
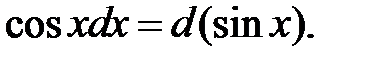
 10.
10. 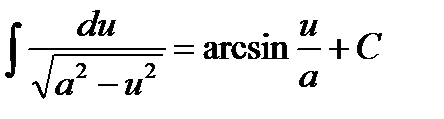
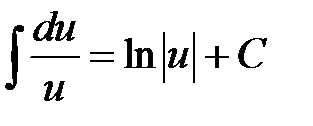 11.
11. 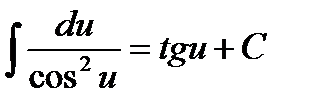
 12.
12. 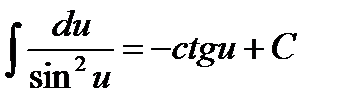
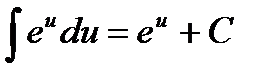 13.
13. 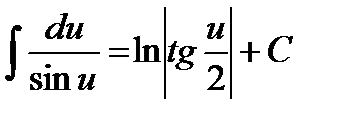
 14.
14. 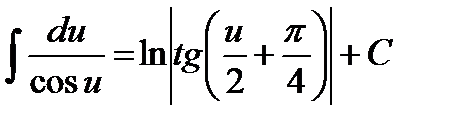
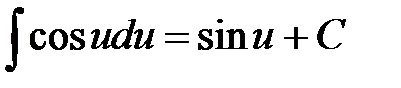 15.
15. 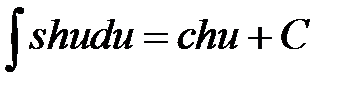
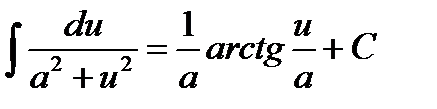 16.
16. 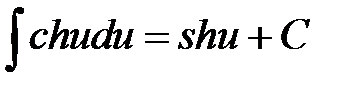
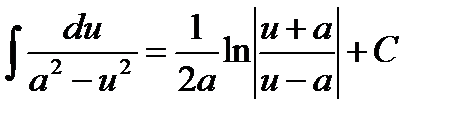 17.
17. 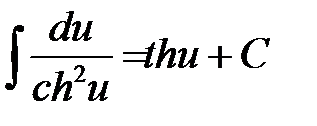
 18.
18.