Означення 1. Функція  називається диференційовною в точці
називається диференційовною в точці  , якщо приріст в ній може бути зображений у вигляді
, якщо приріст в ній може бути зображений у вигляді
 , (5.2)
, (5.2)
де  і
і  – деякі, залежні від
– деякі, залежні від  ,
,  числа, а
числа, а 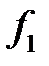 і
і 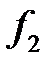 – нескінченно малі коли
– нескінченно малі коли  ,
,  .
.
Означення 2. 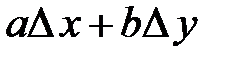 у рівності (5.2) називається головною лінійною частинною приросту функції в точці
у рівності (5.2) називається головною лінійною частинною приросту функції в точці 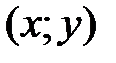 .
.
Означення 3. Диференціалом функції двох змінних називається головна лінійна частина приросту 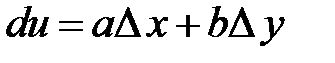 .
.
Теорема. Якщо функція  диференційовна в точці
диференційовна в точці  , то дана функція має частинні похідні по
, то дана функція має частинні похідні по  і
і  в даній точці, а коефіцієнти
в даній точці, а коефіцієнти  і
і  в головній лінійній частині приросту обчислюються за формулами:
в головній лінійній частині приросту обчислюються за формулами:  .
.
Доведення.
За умовою теореми функція  є диференційовною в точці
є диференційовною в точці  . Нехай
. Нехай  . Тоді
. Тоді  ,
,  поділимо рівність на
поділимо рівність на  і знайдемо границю частки, коли
і знайдемо границю частки, коли  :
:
 .
.
Тобто  , аналогічно
, аналогічно  . Що і потрібно було довести.
. Що і потрібно було довести.
Теорема. (Достатня умова диференціювання) Якщо функція двох змінних  має в деякому околі точки, неперервні частинні похідні першого порядку за змінними
має в деякому околі точки, неперервні частинні похідні першого порядку за змінними  та
та  , то повний диференціал функції в цій точці існує і обчислюється за формулою:
, то повний диференціал функції в цій точці існує і обчислюється за формулою:
 . (5.3)
. (5.3)
Приклад 1. Знайти повний диференціал функції  .
.
Розв’язання.
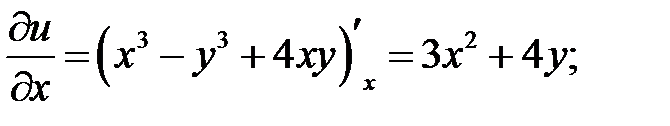

Відповідь:  .
.
Рівність (5.3) використовується для наближеного обчислення значень функції.
Нехай 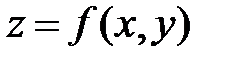 , тоді
, тоді  , тобто:
, тобто:
 .
.
Приклад 2. Обчислити  в т.
в т.  ,
,  .
.
Розв’язання.

Наближене значення:  .
.
Точне значення:  .
.
Відносна похибка:  .
.
Похідна складеної функції  , яка має неперервні частинні похідні за змінними
, яка має неперервні частинні похідні за змінними  в деякому околі т.
в деякому околі т.  , де
, де  ,
,  обчислюється за формулою:
обчислюється за формулою:  . (5.4)
. (5.4)
Приклад 3.  .
. 
Розв’язання.


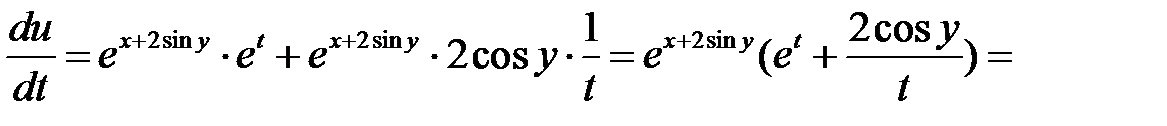

 .
.

 називається диференційовною в точці
називається диференційовною в точці  , якщо приріст в ній може бути зображений у вигляді
, якщо приріст в ній може бути зображений у вигляді , (5.2)
, (5.2) і
і  – деякі, залежні від
– деякі, залежні від  ,
,  числа, а
числа, а 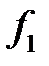 і
і 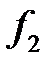 – нескінченно малі коли
– нескінченно малі коли  ,
,  .
.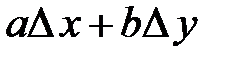 у рівності (5.2) називається головною лінійною частинною приросту функції в точці
у рівності (5.2) називається головною лінійною частинною приросту функції в точці 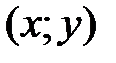 .
.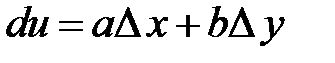 .
. , то дана функція має частинні похідні по
, то дана функція має частинні похідні по  і
і  в даній точці, а коефіцієнти
в даній точці, а коефіцієнти  .
. . Нехай
. Нехай  . Тоді
. Тоді  ,
,  поділимо рівність на
поділимо рівність на  і знайдемо границю частки, коли
і знайдемо границю частки, коли  :
: .
. , аналогічно
, аналогічно  . Що і потрібно було довести.
. Що і потрібно було довести. . (5.3)
. (5.3) .
.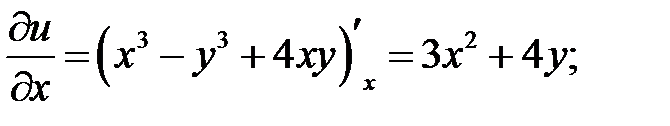

 .
.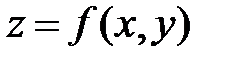 , тоді
, тоді  , тобто:
, тобто: .
. в т.
в т.  ,
,  .
.
 .
. .
. .
. в деякому околі т.
в деякому околі т.  , де
, де  ,
,  обчислюється за формулою:
обчислюється за формулою:  . (5.4)
. (5.4) .
. 


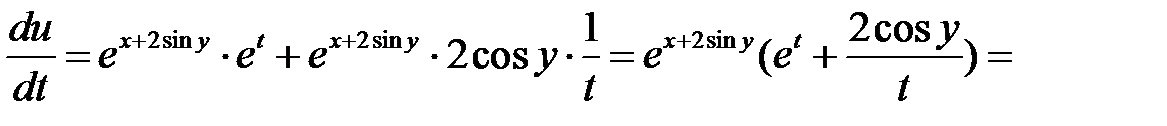

 .
.


