Означення 4. Диференціал від диференціала першого порядку називають диференціалом другого порядку:

 .
.
Аналогічно знаходимо диференціал 3-го та 4-го порядку:  .
.
Зауваження. Теореми про добуток і частку похідної справедливі і для диференціала:  ,
,  . Але для диференціала
. Але для диференціала  порядку вони мають зміст тільки коли
порядку вони мають зміст тільки коли  незалежна змінна. Для складеної функції ці формули не виконуються.
незалежна змінна. Для складеної функції ці формули не виконуються.
Дійсно: 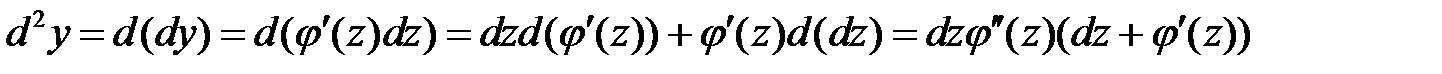
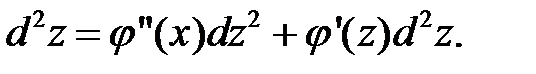
Деякі теореми про диференційовні функції. Правило Лопіталя
Теорема Ферма. (Фр. 1601 – 1665) Нехай функція  визначена на інтервалі
визначена на інтервалі  і приймає в деякій точці
і приймає в деякій точці  найбільше або найменше значення. Тоді якщо в т.
найбільше або найменше значення. Тоді якщо в т.  існує похідна цієї функції, вона дорівнює нулю.
існує похідна цієї функції, вона дорівнює нулю.
Доведення.
Нехай в т.  функція приймає найбільше значення
функція приймає найбільше значення  на інтервалі
на інтервалі  (рис.4.32). Покажемо, що
(рис.4.32). Покажемо, що  .
.
Так як  .
.
Рисунок 4.32
Оскільки в т.  значення найбільше, то звідси випливає, що
значення найбільше, то звідси випливає, що
 i
i 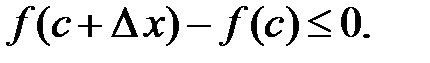
а)  , то
, то 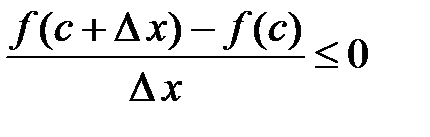 і
і  ;
;
б)  , то
, то  і
і  при
при 
 . Теорему доведено.
. Теорему доведено.
Теорема Ролля. Якщо  неперервна на проміжку
неперервна на проміжку 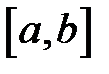 та диференційовна на інтервалі
та диференційовна на інтервалі 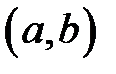 і
і  , то знайдеться точка
, то знайдеться точка  , така, що
, така, що 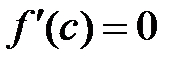 .
.
Теорема Лагранжа. Якщо  неперервна на проміжку
неперервна на проміжку 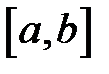 та диференційовна на інтервалі
та диференційовна на інтервалі 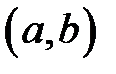 , то існує така точка
, то існує така точка  , що має місце рівність
, що має місце рівність  .
.
Геометричний зміст: на 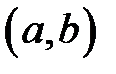 існує точка
існує точка 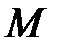 , в якій дотична до графіка
, в якій дотична до графіка  паралельна січній
паралельна січній  (рис.4.33).
(рис.4.33).
Рисунок 4.33
Доведення.
Візьмемо на 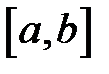 функцію
функцію 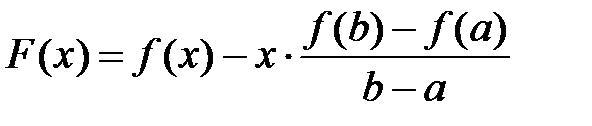 .Так, як вона задовольняє теорему Ролля, то існує точка
.Так, як вона задовольняє теорему Ролля, то існує точка  , така, що:
, така, що:

 .
.
Що і потрібно було довести.


 .
. .
. ,
,  . Але для диференціала
. Але для диференціала  порядку вони мають зміст тільки коли
порядку вони мають зміст тільки коли  незалежна змінна. Для складеної функції ці формули не виконуються.
незалежна змінна. Для складеної функції ці формули не виконуються.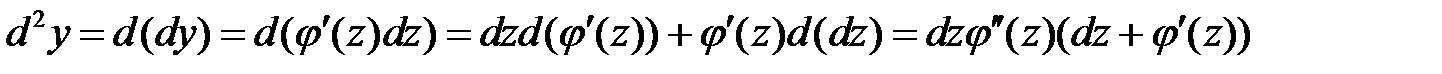
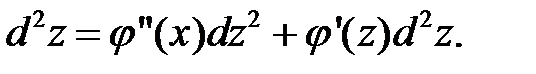
 визначена на інтервалі
визначена на інтервалі  і приймає в деякій точці
і приймає в деякій точці  найбільше або найменше значення. Тоді якщо в т.
найбільше або найменше значення. Тоді якщо в т.  існує похідна цієї функції, вона дорівнює нулю.
існує похідна цієї функції, вона дорівнює нулю.

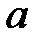



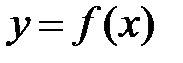
 функція приймає найбільше значення
функція приймає найбільше значення  на інтервалі
на інтервалі  (рис.4.32). Покажемо, що
(рис.4.32). Покажемо, що  .
. .
. i
i 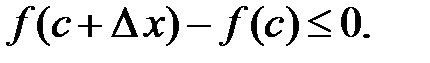
 , то
, то 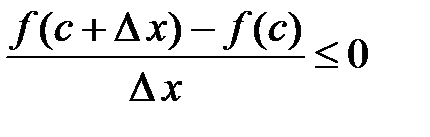 і
і  ;
; , то
, то  і
і 
 . Теорему доведено.
. Теорему доведено. неперервна на проміжку
неперервна на проміжку 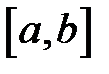 та диференційовна на інтервалі
та диференційовна на інтервалі 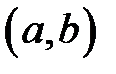 і
і  , то знайдеться точка
, то знайдеться точка  , така, що
, така, що 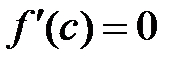 .
. .
.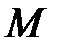 , в якій дотична до графіка
, в якій дотична до графіка  (рис.4.33).
(рис.4.33).



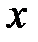



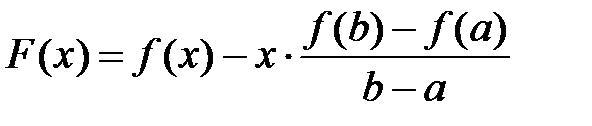 .Так, як вона задовольняє теорему Ролля, то існує точка
.Так, як вона задовольняє теорему Ролля, то існує точка 
 .
.


