Теорема 5. Якщо для функції  існує обернена функція
існує обернена функція  , яка в точці
, яка в точці  має похідну
має похідну  , відмінну від нуля, то в відповідній т.
, відмінну від нуля, то в відповідній т.  функція
функція  має похідну
має похідну 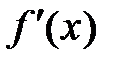 , що дорівнює
, що дорівнює  , тобто
, тобто  .
.
Доведення.
Надамо  деякого приросту
деякого приросту  , тоді
, тоді  . Так як
. Так як  монотонна, то
монотонна, то  . Але
. Але  неперервна, то
неперервна, то  при
при  . Тоді:
. Тоді:  .
.
Що і потрібно було довести.
Нехай функція задана параметричними рівняннями 
 і
і  диференційовні в околі т.
диференційовні в околі т.  , причому
, причому  .
.
Тоді 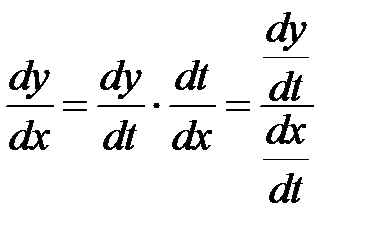 , тобто
, тобто  .
.
Нехай функція задана рівнянням  , а не
, а не  , тобто неявно. Для того, щоб знайти похідну треба продиференціювати обидві частини цього рівняння по
, тобто неявно. Для того, щоб знайти похідну треба продиференціювати обидві частини цього рівняння по  і з отриманого рівняння знайти
і з отриманого рівняння знайти  .
.
Приклад 1. Знайти похідну функції  .
.
Розв’язання.
 ;
; 
 ;
; 

 ;
; 
 ;
; 

 ;
; 
 .
.
Таблиця похідних
Для  має місце:
має місце:



















Рівняння дотичної та нормалі до кривої
Розглянемо криву  . На цій лінії візьмемо т.
. На цій лінії візьмемо т.  (рис.4.30).
(рис.4.30).
Запишемо рівняння дотичної, що проходить через т.

і не паралельна осі

.
Рівняння прямої з даним кутовим коефіцієнтом  , що проходить через т.
, що проходить через т.  має вигляд:
має вигляд: 
Рисунок 4.30  .
.
Означення 1. Нормаллю до кривої в даній точці називається пряма, що проходить через цю точку перпендикулярно до дотичної.
 ;
;  .
.
Довжина відрізка  дотичної називається довжиною дотичної.
дотичної називається довжиною дотичної.
Проекція цього відрізка на вісь  –
–  називається піддотичною. Довжина
називається піддотичною. Довжина  називається довжиною нормалі, а проекція
називається довжиною нормалі, а проекція  називається піднормаллю.
називається піднормаллю.
 і не паралельна осі
і не паралельна осі  .
.

 існує обернена функція
існує обернена функція  , яка в точці
, яка в точці  має похідну
має похідну  , відмінну від нуля, то в відповідній т.
, відмінну від нуля, то в відповідній т.  функція
функція  має похідну
має похідну 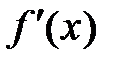 , що дорівнює
, що дорівнює  , тобто
, тобто  .
. деякого приросту
деякого приросту  , тоді
, тоді  . Так як
. Так як  монотонна, то
монотонна, то  . Але
. Але  неперервна, то
неперервна, то  при
при  . Тоді:
. Тоді:  .
.
 і
і  диференційовні в околі т.
диференційовні в околі т.  , причому
, причому  .
.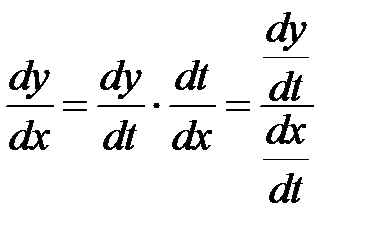 , тобто
, тобто  .
. , а не
, а не  , тобто неявно. Для того, щоб знайти похідну треба продиференціювати обидві частини цього рівняння по
, тобто неявно. Для того, щоб знайти похідну треба продиференціювати обидві частини цього рівняння по  і з отриманого рівняння знайти
і з отриманого рівняння знайти  .
. .
. ;
; 
 ;
;  ;
;  ;
;  ;
;  .
. має місце:
має місце:
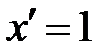


















 . На цій лінії візьмемо т.
. На цій лінії візьмемо т.  (рис.4.30).
(рис.4.30).






 , що проходить через т.
, що проходить через т.  має вигляд:
має вигляд: 
 .
. ;
;  .
. дотичної називається довжиною дотичної.
дотичної називається довжиною дотичної. –
–  називається піддотичною. Довжина
називається піддотичною. Довжина  називається довжиною нормалі, а проекція
називається довжиною нормалі, а проекція  називається піднормаллю.
називається піднормаллю.


