Властивості. 1. Якщо має границю , а – нескінченно велика, то їх відношення прямує до нуля
1. Якщо 2. Якщо Невизначені вирази Вираз якщо якщо Границя функції Означення 1. Число
Рисунок 4.23 Приклад 1. Показати, що Розв’язання. Знайдемо
Означення 2. Число Приклад 2. Показати, що Розв’язання.
Односторонні границі
 називається правосторонньою границею функції називається правосторонньою границею функції 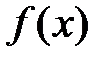 , при , при 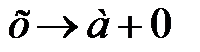 якщо для будь-якого якщо для будь-якого 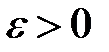 , знайдеться , знайдеться  таке, що таке, що 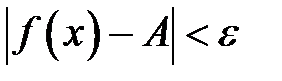 , якщо , якщо 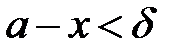 , тобто , тобто  (рис.4.24). Записують (рис.4.24). Записують 
Рисунок 4.24
 називається лівосторонньою границею функції називається лівосторонньою границею функції 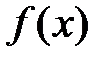 , при , при 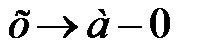 якщо для будь-якого якщо для будь-якого 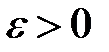 , знайдеться , знайдеться  таке, що таке, що 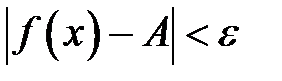 , якщо , якщо 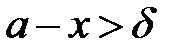 , тобто , тобто  (рис.4.25). (рис.4.25).
Записують Рисунок 4.25 Теорема. Границя функції
Приклад 3. Розв’язання.
Означення 5. Функція
|

 має границю
має границю 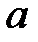 , а
, а  – нескінченно велика, то їх відношення прямує до нуля
– нескінченно велика, то їх відношення прямує до нуля 

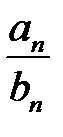 при
при  , при
, при  є невизначеністю виду
є невизначеністю виду  ;
;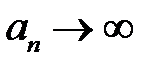 ,
,  маємо невизначеність виду
маємо невизначеність виду 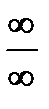 ;
; ,
,  маємо:
маємо:  ; є невизначеності (
; є невизначеності ( ),
),  ,
, 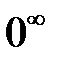 і т.д.
і т.д. , якщо для будь-якого
, якщо для будь-якого  , що як тільки
, що як тільки  , виконується нерівність
, виконується нерівність  , тобто
, тобто . Геометрично: (рис.4.23)
. Геометрично: (рис.4.23)







 .
. , задамо
, задамо  .
.
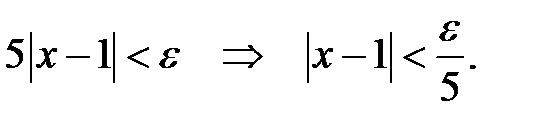

 При
При  .
. , що як тільки
, що як тільки  виконується
виконується  , тобто
, тобто  .
. .
. але
але 

 .
.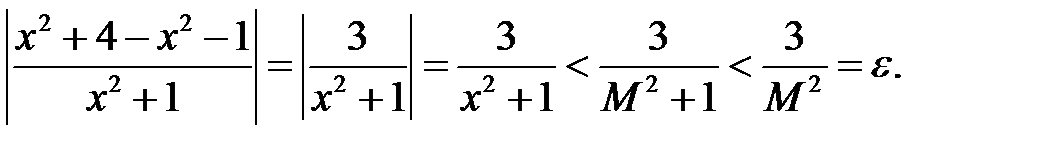 Тобто,
Тобто,  .
.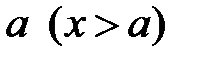

 .
.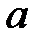 існує тоді і тільки тоді, коли існує ліво- і правостороння границі, і вони рівні:
існує тоді і тільки тоді, коли існує ліво- і правостороння границі, і вони рівні: .
.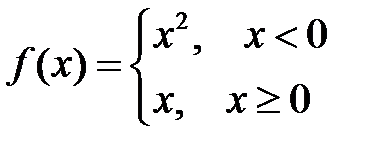
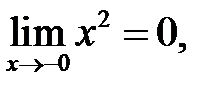

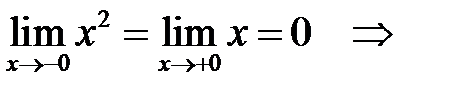 границя існує і дорівнює нулю.
границя існує і дорівнює нулю. , що
, що  для всіх точок з цього інтервалу.
для всіх точок з цього інтервалу.


