Означення 1. Визначником матриці третього порядку
В означенні виражено обчислення визначника матриці за правилом трикутника. Обчислення визначника 3-го порядку за правилом трикутника спростив Саррюс, який запропонував для зручності записати два перших стовпця за третім і обчислювати елементи у трикутниках за напрямом прямих. Правило Саррюса:
Приклад 1. Показати, що визначник Розв’язання.
Зауваження. Всі властивості (1–9) визначників другого порядку, справедливі і для визначників третього порядку. Означення 2. Мінором Мінор першого порядку можна отримати з матриці другого порядку,наприклад: Мінор другого порядку можна отримати з матриці третього порядку, наприклад: Означення 3. Алгебраїчним доповненням (або ад’юнктом) Теорема 1. (Розкладу) Визначник матриці дорівнює сумі добутків елементів деякого рядка (стовпця) на алгебраїчні доповнення цих елементів:
Доведення.
Що і потрібно було довести. Приклад 2. Обчислити визначник розкладом за елементами першого рядка. Перевірити розкладом за елементами другого рядка:
Розв’язання.
Теорема 2. (Анулювання) Сума добутків елементів деякого рядка (стовпця) визначника на відповідні алгебраїчні доповнення елементів іншого рядка (стовпця) дорівнює нулю. Доведення. Візьмемо для доведення, наприклад, елементи третього рядка та алгебраїчні доповнення елементів першого рядка.
Що і потрібно було довести. Обчислення визначника розкладом за елементами
|

 називається число
називається число .
.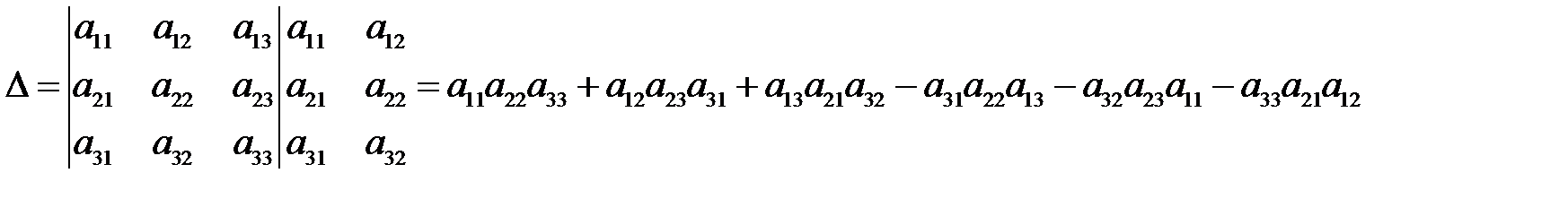 .
.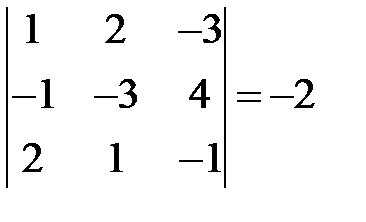 .
.
 .
. елемента
елемента  матриці
матриці  , називається визначник отриманий з матриці
, називається визначник отриманий з матриці  -го рядка та
-го рядка та  -го стовпця.
-го стовпця.

 .
. .
. елемента
елемента  називається мінор цього елемента, взятий із знаком
називається мінор цього елемента, взятий із знаком  , тобто
, тобто  .
. .
.
 .
. .
. .
.
 .
.


