Властивості визначників матриць другого порядку1. Доведення.
2. Якщо елементи будь-якого рядка (стовпця) матриці дорівнюють нулю, то визначник цієї матриці дорівнює нулю: 3. Якщо елементи одного рядка матриці дорівнюють відповідно елементам другого рядка, то визначник цієї матриці дорівнює нулю. 4. Якщо елементи двох рядків поміняти місцями, то визначник не зміниться за абсолютною величиною, а його знак зміниться на протилежний:
5. Якщо елементи деякого рядка матриці помножити на одне і те ж саме число
6. Якщо елементи деякого рядка матриці пропорційні елементам іншого рядка цієї ж матриці, то її визначник дорівнює нулю:
7. Нехай дано два визначники другого порядку в яких відповідно два стовпчики співпали, а два різні:
Сума цих визначників дорівнює визначнику другого порядку, у якого вказаний стовпчик складається із суми відповідних елементів цих стовпчиків:
Дійсно,
8. 9. Якщо до елементів деякого рядка матриці додати відповідно елементи другого рядка матриці, помножені на одне і те ж число Доведення.
Що і потрібно було довести. Наслідок. Будь-яка властивість рядків визначника, має місце і для стовпців. Визначники матриць третього порядку
|
. 
.
.
.
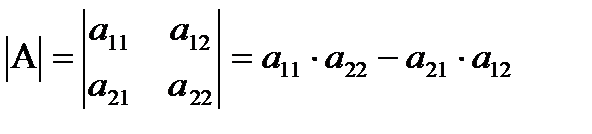, то визначник матриці зміниться в 
.
.
, 
.
.
.
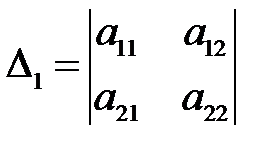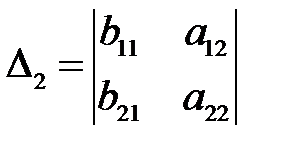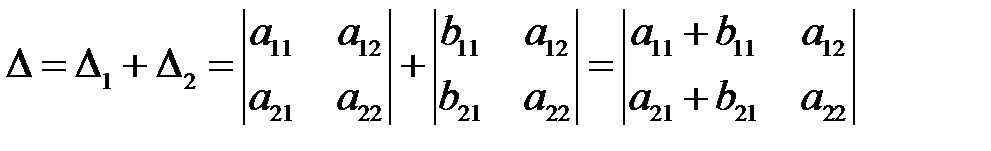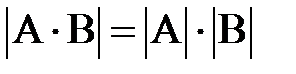
, то визначник матриці не зміниться.
.
