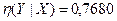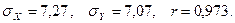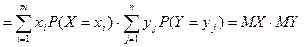Раздел 5.
1. 13/30 2. 11/20, 4/5, 11/100 3. 1 4. m / n 5. 67/120 6. 0,52. Короткое решение. Событие А - вынут белый шар. Гипотезы:
7. 8. 0,78 9. 0,816 11. 20/21 12. 6/7. Указание: полная сумма событий в данном опыте состоит из четырёх гипотез. 13. 2/3, 1/2, 1/3 14. 0,41 15. 0,77, 0,19, 0,04 16. 0,64, 0,16, 0,04
Раздел 6 1. 5/16, 13/16, 1/32 2. 27/128 3. Выиграть 2 встречи из четырёх. Как объяснить это, используя числовые характеристики биномиального распределения? 4. 0,77, 0,02 5. 0,373 6. 0,737 7. 8. Вероятность того, что при n бросаниях «шестёрка» не выпадет ни разу равна а) n ≥ 4, б) n ≥ 13 9. 0,019
Раздел 7 1. 0,0798, 0,011, ≈ 0 2. 0,0532, 0,022 3. 0,052 4. 0,682 5. 0,97 6. 0,972 7. От 4 до 23. Применить правило «трёх сигм». 8. 9. 0,2385 10. 11. 12. 0,1755, 0, 0181, 0,0067, 0,9933 13. а) неравенство для нахождения k: 120000 ≤ 1000 ۰ k,
б) неравенство для нахождения k: 80000 ≥ 1000 ۰ k,
Раздел 8
1. б) в) 0,8, г) 0,2, 1,36, 1,17, 5,85, любая точка в интервале [1, 0], 1 д)
2. б) 3. б) в) 1/2, г) 3/2, 3/4, д)
4. 5. а) 6. а) 7. –3, 160, 8. а) 7/2, 35/12, ≈ 1,71; б) 9. Пусть центр круга радиуса R расположен в начале координат. Если (x, y) – координаты брошенной в круг точки, то
Плотность распределения ξ равна 10.
Раздел 9 1. 2, 1,9, ≈1,38 2. 3,2 3. 0,9938. Использовать интегральную теорему Муавра-Лапласа. 4. 5.
6. 2/9, 1/3, 22,5 7. 0,136, 0,152 8. 0,092 9. 0,081, 0,788 10. 0,192, 0,692, 0,023 11. Да. Применить правило «трёх сигм».
Раздел 10. 1. 1.
2. Являются зависимыми, например, P (X = 2 и Y = -1), но
3.
4.
5. M (Y | X = 2) = -1 · 0,2 + 0 · 0,667 + 1 · 0,133 = -0,067 M (Y | X = 3) = -1 · 0,4 + 0 · 0,4 + 1· 0,2 = -0,2
7.
9.
10.
Замечание. Незначительное превышение величины | r | = 0,092 корреляционного отношения
2. 1.
2. Являются зависимыми: 3. МХ = 57/16 = 3,5625, DX = 1,2461, MY = 57/16 = 3,5625, DY = 0,9980, 4.
(удалить эту сетку)
5. M (Y | X = 2) = 2,5, M (Y | X = 3) = 3, M (Y | X = 4) = 4,2, M (Y | X = 5) = 4,25 7. D (Y | X = 2) = 0,25, D (Y | X = 3) = 0,6667, D (Y | X = 4) = 0,56, D (Y | X = 5) = 0,1875 9. r =0,7251 10. D (Y | X) = 0,4091,
3.
MX = 61, MY = 170, DX = 52,8, DY = 50,
4.
|

 - вынутый из второй урны шар принадлежал первой урне;
- вынутый из второй урны шар принадлежал первой урне;  - вынутый из второй урны шар принадлежал второй урне.
- вынутый из второй урны шар принадлежал второй урне.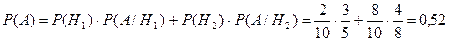


 Решая неравенства
Решая неравенства  получим:
получим:


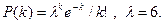


 ,
,
 , в) 1, г) 1/6, 5/36,
, в) 1, г) 1/6, 5/36,  ,
, 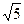 , 0, 0, д)
, 0, 0, д) 
 ,
, , любая точка интервала [1, 2], два значения: 1 и 2,
, любая точка интервала [1, 2], два значения: 1 и 2,

 , б) 0,25, в) 0,75
, б) 0,25, в) 0,75 , б)
, б) 


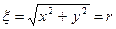 - длина радиус-вектора точки. При
- длина радиус-вектора точки. При  . Поэтому
. Поэтому


 Квадратичное неравенство
Квадратичное неравенство  выполняется при любом значении p.
выполняется при любом значении p.
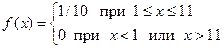
 - любое значение из [1, 11], Dξ = 8,33
- любое значение из [1, 11], Dξ = 8,33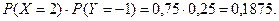

 , поэтому
, поэтому

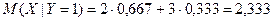

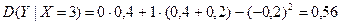

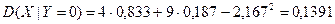
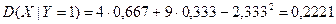





 объясняется ошибками округления в проведённых расчётах.
объясняется ошибками округления в проведённых расчётах.