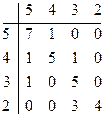Раздел 10. Двумерные случайные величины. Зависимость случайных величин
1. Найти законы распределения случайных величин X и Y. 2. Являются ли случайные величины X и Y независимыми? 3. Найти математические ожидания дисперсии и среднеквадратичные отклонения случайных величин X и Y. 4. Найти условные распределения Y | X = 2, Y | X = 3, X | Y = -1, X | Y = 0, X | Y = 1. 5. Найти условные математические ожидания M (Y | X = 2), M (Y | X = 3), M (X | Y= -1), M (X | Y = 0), M (X | Y = 1). 6. Построить по точкам линии регрессии 7. Найти условные дисперсии D (Y | X =2), D (Y | X =3), D (X | Y = -1), D (X | Y = 0), D (X | Y = 1). 8. Построить по точкам скедастические линии D (Y | X = x) и D (X | Y = y). 9. Найти коэффициент корреляции случайных величин X и Y. 10. Найти корреляционные отношения случайных величин X и Y.
1. Найти законы распределения случайных величин X и Y. 2. Являются ли случайные величины X и Y независимыми? 3. Найти математические ожидания дисперсии и среднеквадратичные отклонения случайных величин X и Y. 4. Найти условные распределения Y | X = 2, Y | X = 3, Y | X = 4, Y | X = 5. 5. Найти условные математические ожидания M (Y | X = 2), M(X | Y =3), M (Y | X = 4), M (Y | X = 5). 6. Построить по точкам линию регрессии 7. Найти условные дисперсии D (Y | X =2), D (Y | X =3), D (Y | X =4), D (Y | X =5). 8. Построить по точкам скедастическую линию D (Y | X = x). 9. Найти коэффициент корреляции случайных величин X и Y. 10. Найти корреляционное отношение
Составить таблицу распределения двумерной случайной величины (X, Y) и найти коэффициент корреляции случайных величин X и Y.
4. Доказать, что для независимых дискретных случайных величин X и Y
Раздел 11. Предварительная обработка выборки. Эмпирическая функция рапределения. Точечные оценки числовых характеристик генеральной совокупности. 1. Из генеральной совокупности Х извлечена выборка объёма n = 10: 6, 3, 3, 4, 6, 1, 4, 3, 1, 6.
1. Записать вариационный ряд выборки. Найти размах выборки. 2. Составить таблицу эмпирического (выборочного) распределения 3. Найти статистические ряды частот и относительных частот выборки. Оценить вероятности Р (Х = 3), Р (Х = 4), Р (Х = 5). 4. Построить гистограммы частот и относительных частот выборки. Сформулировать гипотезу о типе распределения генеральной совокупности. 5. Найти эмпирическую функцию распределения. Оценить вероятности 6. Найти точечные оценки числовых характеристик генеральной совокупности.
2. Размах выборки оказался равным 0. Какое предположение о генеральной совокупности наиболее естественно?
3. Тестирование знаний 30 студентов дало следующий результат:
1 балл получил 1 студент, 2 балла получили 5 студентов 3 балла - 10 студентов 4 балла - 9 студентов 5 баллов - 3 студента 6 баллов - 2 студента.
Считаем результат этого теста случайной выборкой из генеральной совокупности – уровня знаний студентов всего курса.
67 65 39 48 43 54 60 42 50 59 59 54 57 14 49 48 46 47 68 52 61 30 58 32 42 58 49 77 28 47 45 44 30 55 40 41 72 47 61 35 42 33 45 51 21 41 53 60 38 60.
1. Найти группированные статистические ряды частот и относительных частот выборки при её группировке в 7 интервалов (размах выборки равен 63). 2. Построить гистограмму частот группированной выборки. Сформулировать гипотезу о типе распределения генеральной совокупности. 3. Найти точечные оценки числовых характеристик генеральной совокупности.
Найти выборочное среднее и несмещённую оценку дисперсии.
1)
2)
где
Первый опыт. Производится одно бросание монеты. При выпадении герба «блуждающая точка» смещается по оси Ох на 1 единицу вправо, т.е.
Второй опыт. Производится одно бросание монеты. При выпадении герба «блуждающая точка» смещается в точку
i - ый опыт. Производится одно бросание монеты.
Таким образом проводится серия из N опытов, в результате которой формируется генеральная совокупность X.
Требуется: 1. Смоделировать описанной выше серией из 50 опытов выборку объёмом n = 50 из генеральной совокупности X. 2. Построить статистический ряд частот и гистограмму выборки. 3. Сформулировать гипотезу о типе распределения генеральной совокупности. 4. Вычислить выборочное среднее.
Раздел 12. Доверительный интервал 1. Сделано 4 измерения расстояния от орудия до цели дальномером с точностью σ = 40м. Среднее выборочное этих 4 измерений равно 2000 м. Найти доверительный интервал для оценки истинного расстояния до цели при доверительной вероятности 0,95. Установить, сколько надо измерений, чтобы с той же вероятностью 0,95 точность оценки расстояния до цели составила 10м.
2. При исследовании содержания чистого серебра в 10 монетах «рубль», чеканившихся в Росcии с 1730 г по 1761 г, получена средняя величина 20,75г. Оценить истинное значение содержания серебра в монете «рубль» этого периода при уровне значимости 0,1, если среднеквадратичная погрешность применённого для анализа метода составляла 0,1г.
3. Для данных из условия задачи №4 из раздела 11 найти доверительный интервал для выборочного среднего при уровне значимости 0,2. Среднеквадратичное отклонение в генеральной совокупности считать равным 13с.
4. При тестировании общего интеллекта у 25 человек получен средний балл 45. Считая, что общий интеллект имеет нормальное распределение со среднеквадратичным отклонением 16 баллов, найти доверительную вероятность, при которой этот средний балл получен с точностью до 3 баллов, 5 баллов, 8 баллов.
5. Игровой автомат должен обеспечивать в среднем один выигрыш в ста играх. При его проверке в 400 играх было 5 выигрышей. Найти доверительный интервал для неизвестной вероятности выигрыша при доверительной вероятности 0,95. Указание. При большом объёме выборки n границы доверительного интервала
Раздел 13. Проверка статистических гипотез
а) По двухстороннему биномиальному критерию при уровне значимости α = 0,05 проверить гипотезу б) По левостороннему биномиальному критерию при уровне значимости α = 0,01 проверить гипотезу
Проверить для уровня значимости 0,1, что метод даёт случайные числа, то есть распределение цифр равномерное.
Можно ли считать поток микрометеоритов равномерным за время наблюдения? Уровень значимости взять равным 0,05.
.
Указание. В расчёте объединить интервалы 1 и 2, 6 и 7.
а)
б)
Оценки на экзамене
Оценки за семестр
Взять уровень значимости 0,01.
Группа 1 33, 19, 34, 25, 24; Группа 2 32, 24, 28, 16.
Считая, что оценки по данному тесту имеют нормальное распределение, проверить гипотезу о равенстве средних оценок в этих группах. Взять уровень значимости 0,1.
КР1: 4 2 2 2 2 5 4 2 2 2 2 2 5 4 2 2 КР2: 5 4 4 2 2 5 4 2 2 3 4 2 5 4 3 4
Проверить при уровне значимости 0,01, улучшилась ли подготовка студентов ко второй контрольной работе.
Ответы
|

 и
и  .
.

 .
. .
.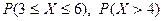 .
.


 , которое случайная величина X принимает в i -ом опыте, является абсциссой так называемой «блуждающей (по оси Ox) точки.» Перед первым опытом «блуждающая точка» находится в точке 0 на оси Ох.
, которое случайная величина X принимает в i -ом опыте, является абсциссой так называемой «блуждающей (по оси Ox) точки.» Перед первым опытом «блуждающая точка» находится в точке 0 на оси Ох.  , а при выпадении цифры «блуждающая точка» смещается по оси Ох на 1 единицу влево, т.е.
, а при выпадении цифры «блуждающая точка» смещается по оси Ох на 1 единицу влево, т.е. 
 , а при выпадении цифры – в точку
, а при выпадении цифры – в точку 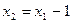 . Таким образом,
. Таким образом,  принимает одно из значений -2, 0, 2.
принимает одно из значений -2, 0, 2. , если выпал герб, или
, если выпал герб, или  , если выпала цифра.
, если выпала цифра. находятся по приближённым формулам
находятся по приближённым формулам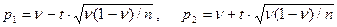 , где ν – точечная оценка параметра p по выборке,
, где ν – точечная оценка параметра p по выборке,  - квантиль нормального распределения N (0, 1).
- квантиль нормального распределения N (0, 1). . Произведя 100 наблюдений, экспериментаторы получили 39 совпадений выбранных прямоугольников. Проверить по правостороннему биномиальному критерию гипотезу
. Произведя 100 наблюдений, экспериментаторы получили 39 совпадений выбранных прямоугольников. Проверить по правостороннему биномиальному критерию гипотезу  о том, что в данном опыте телепатия не проявилась, при значениях уровня значимости α = 0,05 и α = 0,15.
о том, что в данном опыте телепатия не проявилась, при значениях уровня значимости α = 0,05 и α = 0,15.