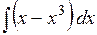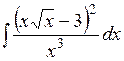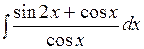Основные свойства неопределенного интеграла
Проинтегрировать функцию
Рассмотрим следующие примеры:
1). Найти интеграл
Разделив почленно числитель на знаменатель, разложим подынтегральную функцию на слагаемые, после чего проинтегрируем каждое из полученных выражений:
Через С обозначен результат суммирования всех произвольных постоянных, получающихся при интегрировании каждого слагаемого.
2). Вычислить интеграл
Представим подынтегральную функцию следующим образом:
Тогда
3). Найти интеграл
Представим подынтегральную функцию в таком виде:
Подставим полученное выражение:
4). Вычислить интеграл
Преобразуем подынтегральную функцию таким образом:
Подставляя полученную функцию, вычисляем интеграл:
Используя правила интегрирования и таблицу интегралов найти следующие интегралы:
|
или 
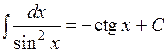
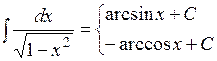
значит найти её неопределенный интеграл. Непосредственное интегрирование основано на прямом использовании основных свойств неопределенного интеграла и таблицы простейших интегралов.
.
