Дифференциал функции
Дифференциалом (первого порядка) функции Дифференциалом аргумента называется приращение этого аргумента: Дифференциал функции равен произведению ее производной на дифференциал аргумента:
Основные свойства дифференциала.
1. 2. 3. 4. 5. 6.
Если приращение аргумента Дифференциалом второго порядка функции Используя определение дифференциала, рассмотрим ряд примеров. 1. Найти приращение Имеем
Найдем дифференциал функции:
Абсолютная погрешность
Относительная погрешность
2. Найти дифференциалы первого и второго порядков функции Имеем
3. Вычислить приближенное значение Рассмотрим функцию
4. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м. Воспользуемся формулой
Следовательно, площадь круга радиуса 3,02м имеет приближенное значение
5. Вычислить приближенно Рассмотрим функцию Тогда, воспользовавшись формулой найдем
Таким образом, 6. На сколько увеличилось ребро куба, если объем его изменился с 27 м3 до 27,2 м3? Если Приращение
Найти дифференциалы следующих функций:
Найти дифференциалы первого, второго и третьего порядков.
2.149. Найти приращение и дифференциал функции 2.150. Вычислить 2.151. Найти приращение и дифференциал функции (Ответ: 2.152. На сколько измениться сторона квадрата, если его площадь уменьшится с 16 м2 до 15,82 м2? (Ответ:0,0225 м) 2.153. Найти приближенное значение объема шара радиусом R=2,01 м. (Ответ:34,04 м3). 2.154. Найти приближенное значение 2.155. Найти приближенное значение 2.156. Найти приближенное значение 2.157. Найти приближенное значение 2.158. Поверхностная энергия жидкости рассчитывается по формуле: 2.159. Резиновый шар наполняется газом. Найти приближенно абсолютное и относительное изменение поверхности шара при увеличении его радиуса от 10,0 см до 10,5 см. (Ответ:
2.160. Период колебания математического маятника 2.161. Разность потенциалов между внутренней частью клетки и внешней средой обусловлена различием концентрации ионов внутри Рассчитать изменение
|

 называется главная часть ее приращения, линейная относительно приращения аргумента.
называется главная часть ее приращения, линейная относительно приращения аргумента.

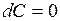 , где С=const
, где С=const
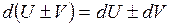

 ,
, 

 мало по абсолютной величине, то
мало по абсолютной величине, то  и
и  . Полученное выражение позволяет использовать дифференциал функции для приближенных вычислений.
. Полученное выражение позволяет использовать дифференциал функции для приближенных вычислений. . Аналогично определяется дифференциал третьего и более высоких порядков.
. Аналогично определяется дифференциал третьего и более высоких порядков. и дифференциал
и дифференциал  функции
функции  при
при  и
и 
 .
. .
.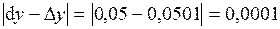 .
. .
. .
.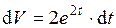 - дифференциал первого порядка,
- дифференциал первого порядка, - дифференциал второго порядка.
- дифференциал второго порядка. .
. . Полагая
. Полагая  ,
,  и применяя формулу
и применяя формулу 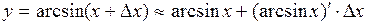 , получаем
, получаем .
. . Полагая R =3,
. Полагая R =3,  , имеем
, имеем .
. .
. .
. и положим x=8,
и положим x=8, 
 ,
,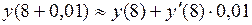 .
. .
. - ребро куба, то его объем
- ребро куба, то его объем  . Задача сводится к отысканию приращения
. Задача сводится к отысканию приращения  при
при  и
и  .
. . Подставляем соответствующие значения и получаем
. Подставляем соответствующие значения и получаем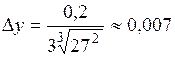 (м).
(м). (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ
(Ответ  )
)
 Ответ:
Ответ:  ;
; 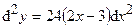 ;
;  .
.
 Ответ:
Ответ: 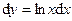 ;
;  ;
; 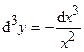 .
.
 Ответ:
Ответ:  ;
;  ;
;  .
.
 Ответ:
Ответ:  ;
;  ;
; 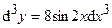 .
.
 при
при  и
и  Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. (Ответ:
Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. (Ответ:  ;
;  ;
;  ).
). для функции
для функции  при
при  ;
;  ).
). при
при  и
и  ;
; 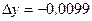 ;
;  ;
;  ).
).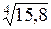 . (Ответ:
. (Ответ:  )
) .(Ответ:2,999)
.(Ответ:2,999) .(Ответ:1,035)
.(Ответ:1,035) . (Ответ:0,88)
. (Ответ:0,88) . Здесь
. Здесь  - энергия единицы площади, равная коэффициенту поверхностного натяжения,
- энергия единицы площади, равная коэффициенту поверхностного натяжения,  - площадь свободной поверхности жидкости. Найти изменение поверхностной энергии мыльного пузыря при увеличении его радиуса с 5 см до 5,2 см (площадь поверхности сферы
- площадь свободной поверхности жидкости. Найти изменение поверхностной энергии мыльного пузыря при увеличении его радиуса с 5 см до 5,2 см (площадь поверхности сферы  ). Коэффициент поверхностного натяжения мыльной воды в условиях данной задачи принять равным 0,04 Дж/м2 . (Ответ:
). Коэффициент поверхностного натяжения мыльной воды в условиях данной задачи принять равным 0,04 Дж/м2 . (Ответ:  Дж).
Дж).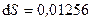 м2;
м2;  )
) , где
, где 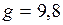 м/с2, а
м/с2, а  см. Найти изменение периода колебаний при уменьшении длины на 1 см. (Ответ:
см. Найти изменение периода колебаний при уменьшении длины на 1 см. (Ответ:  с)
с) и вне
и вне  клетки. Величина этой разности потенциалов в милливольтах для одновалентных ионов при температуре 180 определяется формулой
клетки. Величина этой разности потенциалов в милливольтах для одновалентных ионов при температуре 180 определяется формулой  , где
, где  .
. при увеличении
при увеличении 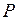 от 20 до 22. Учесть, что
от 20 до 22. Учесть, что  . (Ответ:
. (Ответ:  мВ).
мВ).


