Глава 2.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ Понятие производной Пусть Производной от функции
Или
Примечание. Производная обозначается также как Отыскание производной называется дифференцированием функции. Исходя из определения производной, можно найти производную любой дифференцируемой функции. Рассмотрим несколько примеров. 1. Найти производную функции
Дадим
отсюда
Функция
= Находим отношение приращения функции к приращению аргумента:
Найдем предел этого отношения при
Следовательно, по определению производной
2. Найти производную функции
Находим приращение функции
Таким образом,
Итак,
3. Найти производную функции
Находим приращение функции
Воспользуемся формулой
Отсюда
и
Итак,
Исходя из определения производной, найти производные следующих функций:
|
и 
- два значения аргумента, а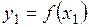 
и 
- соответствующие значения функции 
. Тогда разность 
называется приращением аргумента, а разность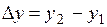 
= 
- приращением функции на отрезке 
.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
(Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по 
.
(1)
, тогда 
получит приращение 
:
,
.
=
= 
.
:
= 
(
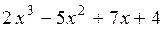(2)
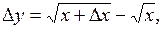отсюда
и
(3)
= 
.
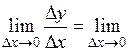
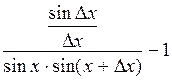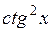
(Ответ: - 
)
(Ответ: 
)
(Ответ: 
)
. (Ответ: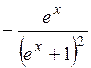 
)
(Ответ: 
)
.
(Ответ: 
)
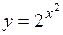Ответ: 
)
.
(Ответ: 6(x-1))
