Дифференцирование сложной функции.
Пусть
Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих. Рассмотрим несколько примеров нахождения производной сложной функции. Пример 1.
Положим Тогда
Пример 2.
Обозначим По правилу дифференцирования сложной функции имеем:
Пример 3.
Обозначим По правилу дифференцирования сложной функции имеем:
Пример 4.
Положим
Пример 5.
Если
Пример 6.
Положим Получаем
Пример 7.
Если
Пример 8.
Имеем
Найти производные следующих сложных функций:
|

 и
и  - дифференцируемые функции. Тогда сложная функция
- дифференцируемые функции. Тогда сложная функция  есть также дифференцируемая функция, причем
есть также дифференцируемая функция, причем .
.
 , где
, где  .
. .
. .
. . Тогда
. Тогда  .
. .
. .
. . Тогда
. Тогда  =
=  .
. .
. . Тогда
. Тогда  .
.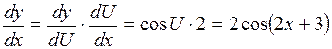 .
.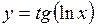 .
. , то
, то  . Следовательно
. Следовательно .
. .
. , где
, где  , а
, а  .
. =
=  .
.
 <1.
<1. то
то  , следовательно,
, следовательно, Выполним алгебраические преобразования и получим окончательно
Выполним алгебраические преобразования и получим окончательно .
.

 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 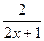 )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
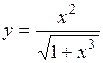 (Ответ:
(Ответ:  )
)

 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 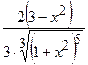 )
)
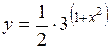 (Ответ:
(Ответ: 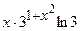 )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 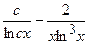 )
)
 (Ответ:
(Ответ: 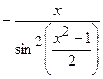 )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
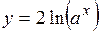 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 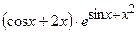 )
)
 (Ответ:
(Ответ: 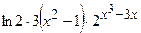 )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
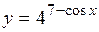 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 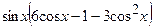 )
)



