При 
 >0 - функция возрастает,
>0 - функция возрастает,
при 
 <0 - функция убывает,
<0 - функция убывает,
при 
 >0 - функция возрастает,
>0 - функция возрастает,
при 
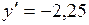 <0 - функция убывает.
<0 - функция убывает.
4.32 Найти интервалы возрастания и убывания функции  , если
, если 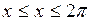 .
.
Решение.
Найдем производную заданной функции: 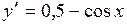 . В промежутке
. В промежутке  производная
производная  >0 поэтому функция возрастает, а в промежутках
>0 поэтому функция возрастает, а в промежутках  и
и  производная
производная  <0 – функция убывает.
<0 – функция убывает.
4.33 Определить характер монотонности функции  в промежутке
в промежутке  .
.
Решение.
Найдем производную:  . При
. При 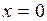 производная
производная  >0 функция возрастает. При
>0 функция возрастает. При  производная
производная  >0 – функция возрастает. Следовательно, функция возрастает во всей области определения.
>0 – функция возрастает. Следовательно, функция возрастает во всей области определения.
Решить следующие задачи.
a. Убедиться, что функция  в интервале
в интервале 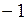 <
<  <3 убывает.
<3 убывает.
b. Определить интервалы убывания и возрастания функции  . (Ответ: при x<0 функция убывает, при x>0 - возрастает.)
. (Ответ: при x<0 функция убывает, при x>0 - возрастает.)
c. Определить, при каких значениях  функция
функция  убывает.
убывает.
(Ответ: при любом  функция убывает).
функция убывает).
d. Проверить, во всем ли интервале  функция
функция 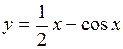 возрастает. (Ответ: при
возрастает. (Ответ: при  функция убывает).
функция убывает).
e. Определить интервал возрастания функции  . (Ответ: при x>0 функция возрастает).
. (Ответ: при x>0 функция возрастает).
f. Найти интервалы возрастания и убывания функции  . (Ответ: в интервале
. (Ответ: в интервале  и
и  функция возрастает; в интервале
функция возрастает; в интервале  - убывает).
- убывает).
g. Найти интервалы монотонности функции  . (Ответ: интервал возрастания
. (Ответ: интервал возрастания  , интервал убывания
, интервал убывания  )
)


 >0 - функция возрастает,
>0 - функция возрастает,
 <0 - функция убывает,
<0 - функция убывает,

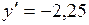 <0 - функция убывает.
<0 - функция убывает. , если
, если 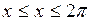 .
.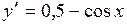 . В промежутке
. В промежутке  производная
производная  >0 поэтому функция возрастает, а в промежутках
>0 поэтому функция возрастает, а в промежутках  и
и  производная
производная  в промежутке
в промежутке  .
. . При
. При 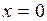 производная
производная  >0 функция возрастает. При
>0 функция возрастает. При  производная
производная  >0 – функция возрастает. Следовательно, функция возрастает во всей области определения.
>0 – функция возрастает. Следовательно, функция возрастает во всей области определения. в интервале
в интервале 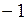 <
<  <3 убывает.
<3 убывает. . (Ответ: при x<0 функция убывает, при x>0 - возрастает.)
. (Ответ: при x<0 функция убывает, при x>0 - возрастает.) убывает.
убывает. функция убывает).
функция убывает). функция
функция 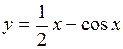 возрастает. (Ответ: при
возрастает. (Ответ: при  функция убывает).
функция убывает). . (Ответ: при x>0 функция возрастает).
. (Ответ: при x>0 функция возрастает). . (Ответ: в интервале
. (Ответ: в интервале  и
и  функция возрастает; в интервале
функция возрастает; в интервале  - убывает).
- убывает). . (Ответ: интервал возрастания
. (Ответ: интервал возрастания  , интервал убывания
, интервал убывания 


