Интегрирование по частям.
С помощью формулы интегрирования по частям
где u, v –дифференцируемые функции, зависящие от х, нахождение интеграла Например: 1). Найти интеграл
Положим
тогда
Отсюда
Используя формулу интегрирования по частям, получим
2). Найти интеграл
Полагая
найдем
Отсюда
3). Найти интеграл
Полагая
получим
Тогда интеграл примет вид:
Используя формулу интегрирования по частям, найти следующие интегралы:
§4. Применение неопределенного интеграла при решении прикладных задач. Рассмотрим задачи. 1). Шкив вращается вокруг оси под действием момента сил М, который меняется с течением времени по закону М=Аt, А - известная постоянная величина. Найти угловую скорость w и угол поворота jшкива в любой момент времени, если в начальный момент шкив был неподвижен. Момент инерции шкива равен I. Используем для решения основное уравнение динамики вращения тела
Отсюда Угловую скорость находим интегрированием последнего выражения, т.е.
Постоянную интегрирования С найдем из начальных условий, т.е. из условия, что при t =0, w=0. Получаем, что С =0. Таким образом, угловая скорость в любой момент времени равна
Учитывая, что угловая скорость и угловой путь связаны формулой
найдем угловой путь
где С- постоянная интегрирования, которая вновь определяется из начального условия: при t =0, w=0, значит С 1=0. Следовательно, угол поворота шкива в любой момент времени равен
2). Скорость тела через t с после начала движения равна V =(4 t +5) м/с. Определить путь, пройденный телом за t с после начала отсчета. Учтя, что
Постоянную интегрирования найдем из начального условия, что при t =0 тело покоилось, следовательно С =0. Тогда окончательно имеем S =2 t 2+5 t (м).
Решить следующие задачи.
4.78 Скорость тела через t с после начала движения равна V=V 0 +at ( м/с). Определить путь, пройденный телом за это время. 4.79 Скорость прямолинейного движения тела в любой момент времени t равна V= 3 t 2 + 4 t (м/с). Найти расстояние, пройденное телом в любой момент времени от начала отсчета, если через 2 с оно равно 15 м. 4.80 В любой момент времени ускорение тела а = 4.81 В любой момент времени скорость тела V= p×cosp t ( м/с). Найти закон движения тела, зная, что в момент времени t =2с пройденное от начала отсчета расстояние равно4 м. 4.82 Сила, действующая на тело в направлении движения, меняется со временем по закону F =6 t (Н). Найти скорость тела в любой момент времени, зная, что в момент начала отсчета она была равна 1 м/с. Масса тела 3 кг. 4.83 На диск действует постоянный вращающий момент силы М =2Н×м. Найти закон изменения угловой скорости и угла поворота диска с течением времени, если в начальный момент времени угловая скорость была 30 рад/с, а угол поворота равен нулю. Момент инерции диска 0,02кг×м2. 4.84 Ток в цепи, содержащей конденсатор, меняется по закону I = Imax sinw t (А), где Imax и w- постоянные величины. Как изменяется со временем заряд конденсатора, если в момент времени, когда ток максимален, заряд равен нулю? 4.85 Скорость тела, брошенного вертикально вверх с начальной скоростью V 0, определяется по формуле V = V 0- gt (м/с). На каком расстоянии от начального положения будет находиться тело через t с после броска?
|


 сводится к отысканию более простого интеграла
сводится к отысканию более простого интеграла  .
. .
. ,
, .
.
 .
.
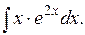



 .
.








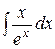



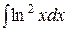
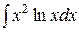

 .
.
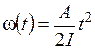 .
. ,
, ,
,

 , получим
, получим 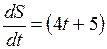 . Тогда
. Тогда .
. (м/с2).Найти зависимость пройденного пути от времени движения, зная, что тело начинает двигаться из состояния покоя с начальной скоростью 3 м/с.
(м/с2).Найти зависимость пройденного пути от времени движения, зная, что тело начинает двигаться из состояния покоя с начальной скоростью 3 м/с.


