ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§1.Основные понятия. Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется дифференциальным уравнением. Порядком дифференциального уранения называется порядок старшей производной, входящей в это уравнение. Например, уравнение Функция y =j(x), удовлетворяющая дифференциальному уравнению, называется решением этого уравнения. Решение дифференциального уравнения, содержащее столько независимых произвольных постоянных, каков порядок уравнения, называется общим решением этого уравнения. Например, для уравнения первого порядка общее решение имеет вид y =j(x,с). Функции, получаемые из общего решения при различных числовых значениях произвольных постоянных, называются частными решениями. Для нахождения частного решения дифференциального уравнения задаются начальные условия. Рассмотрим следующие примеры. 1). Проверить, является ли функция y=cosx решением уравнения y²+y=0. Найдем y¢=-sinx, y²=-cosx. Подставляя выражения для y² и y в данное уравнение, получаем y²+y=-cosx+cosx=0, т.е. функция y=cosx является решением данного дифференциального уравнения. 2). Общее решение дифференциального уравнения y¢-3y=0 иммет вид y=Ce3x. Найти его частное решение, удовлетворяющее начальному условию y(1)=e3. Значение произвольной постоянной С, соответствующее некому частному решению, получается в результате подстановки в выражение общего решения заданных начальных условий: e3=Ce3, откуда С=1. Подставляя полученное значение С=1 в общее решение, найдем частное решение y=e3x, удовлетворяющее заданным начальным условиям.
6.1 Выяснить, являются ли решениями дифференциального уравнения
5.1. 5.2. 5.3. 5.4.
6.2 Выяснить, являются ли решениями дифференциального уравнения 1. 2. 3. 4. 6.3 Общее решение дифференциального уравнения Найти частное решение, удовлетворяющее начальным условиям
|

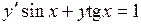 - первого порядка.
- первого порядка.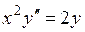 следующие функции:
следующие функции: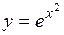 ;
; ;
;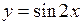 ;
;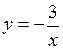 .
.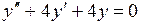 следующие функции:
следующие функции: ;
;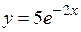 ;
;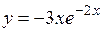 ;
; .
. .
.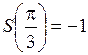 .
.


