Основные правила дифференцирования.
Дифференцирование основных элементарных функций. Основные правила дифференцирования Пусть C –постоянная, 1. 2. 3. 4. 5. Таблица производных основных элементарных функций
Применяя формулы и правила дифференцирования, найдем производную функции:
Запишем данную функцию следующим образом:
Тогда
В качестве следующего примера найдем производную от функции
Для нахождения производной воспользуемся правилом нахождения производной от произведения двух функций:
И, наконец, рассмотрим еще один пример: нахождение производной частного от деления двух функций
Для нахождения производной воспользуемся пятым правилом из раздела «Основные правила дифференцирования». Тогда
Найти производные следующих функций:
|

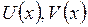 - функции, имеющие производные, тогда:
- функции, имеющие производные, тогда:
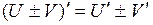
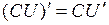
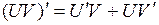
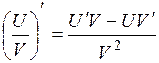





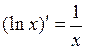
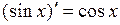



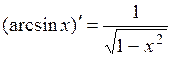
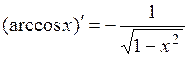

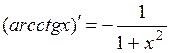
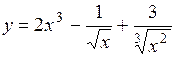


 .
.
 .
.
 .
(Ответ: 6(x-1))
.
(Ответ: 6(x-1))
 .
(Ответ:
.
(Ответ: 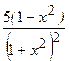 )
)
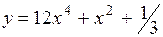 .
(Ответ: 2x(24x2+1))
.
(Ответ: 2x(24x2+1))
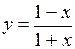 .
(Ответ:
.
(Ответ: 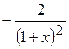 )
)
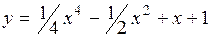 .
(Ответ:
.
(Ответ: 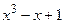 )
)
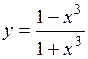 .
(Ответ:
.
(Ответ: 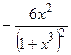 )
)
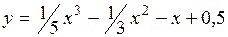 .
(Ответ:
.
(Ответ: 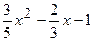 )
)
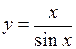 .
(Ответ:
.
(Ответ: 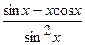 )
)
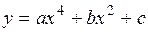 .
(Ответ: 4
.
(Ответ: 4 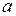
 )
)
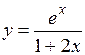 .
(Ответ:
.
(Ответ: 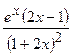 )
)
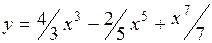 .
(Ответ:
.
(Ответ:  )
)
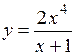 .
(Ответ:
.
(Ответ: 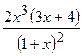 )
)
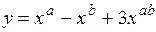 .
(Ответ:
.
(Ответ: 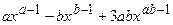 )
)
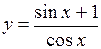 .
(Ответ:
.
(Ответ: 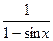 )
)
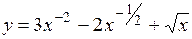 .
(Ответ:
.
(Ответ:  )
)
 (Ответ:
(Ответ: 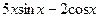 )
)
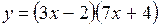 .
(Ответ:
.
(Ответ: 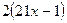 )
)
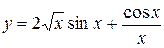 .
(
.
( )
)
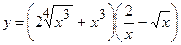 .
(
.
( )
)
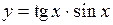 .
(Ответ:
.
(Ответ: 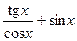 )
)
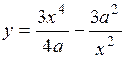 .
(Ответ:
.
(Ответ: 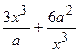 )
)
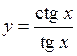 .
(Ответ: -
.
(Ответ: - 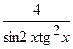 )
)
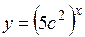 .
(Ответ:
.
(Ответ:  )
)
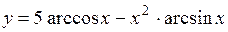 (Ответ:
(Ответ: 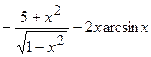 )
)
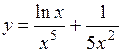 .
(Ответ:
.
(Ответ: 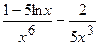 )
)
 .
(Ответ: -
.
(Ответ: - 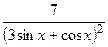 )
)
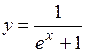 .
(Ответ:
.
(Ответ: 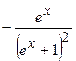 )
)
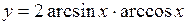 .
(Ответ:
.
(Ответ:  )
)
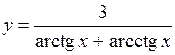 .
(Ответ: 0)
.
(Ответ: 0)
 .
(Ответ:
.
(Ответ: 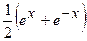 )
)
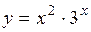 .
(Ответ:
.
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
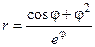 .
(Ответ:
.
(Ответ: 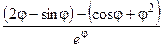 )
)
 .
(Ответ:
.
(Ответ: 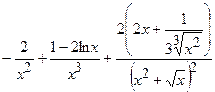
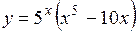 .
(Ответ:
.
(Ответ: 
 )
)
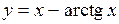 (Ответ:
(Ответ: 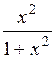 )
)
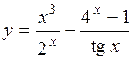 .
.
 )
)
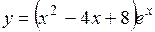 .
(Ответ:
.
(Ответ: 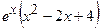 )
)
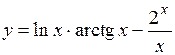 .
(Ответ:
.
(Ответ: 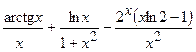 )
)
 .
(Ответ:
.
(Ответ: 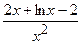 )
)
 .
(Ответ:
.
(Ответ: 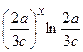 )
)
 .
(Ответ:
.
(Ответ:  )
)
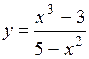 .
(Ответ:
.
(Ответ:  )
)
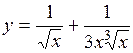 .
(Ответ:
.
(Ответ:  )
)
 .
(Ответ:
.
(Ответ: 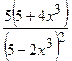 )
)
 .
(Ответ:
.
(Ответ: 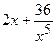 )
)
 .
(Ответ:
.
(Ответ: 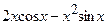 )
)
 .
(Ответ:
.
(Ответ:  )
)
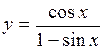 .
(Ответ:
.
(Ответ:  )
)
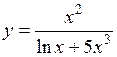 .
(Ответ:
.
(Ответ: 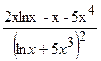 )
)
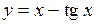 .
(Ответ:
.
(Ответ:  )
)
 .
(Ответ:
.
(Ответ: 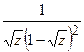 )
)
 .
(Ответ:
.
(Ответ:  )
)
 .
(Ответ:
.
(Ответ: 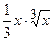 )
)
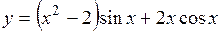 (Ответ:
(Ответ: 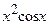 )
)
 .
(Ответ:
.
(Ответ: 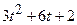 )
)
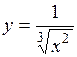 .
(Ответ:
.
(Ответ: 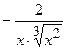 )
)
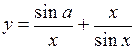 .
(Ответ:
.
(Ответ:  )
)
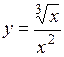 .
(Ответ:
.
(Ответ: 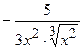 )
)
 .
(Ответ:
.
(Ответ: 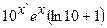 )
)
 .
(Ответ:
.
(Ответ: 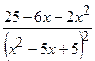 )
)
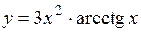 .
(Ответ:
.
(Ответ:  )
)
 .
(Ответ:
.
(Ответ: 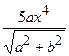 )
)
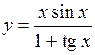 (Ответ:
(Ответ: 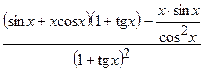 )
)
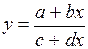 .
(Ответ:
.
(Ответ: 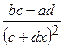 )
)
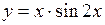 (Ответ:
(Ответ: 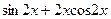 )
)
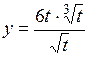 .
(Ответ:
.
(Ответ: 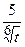 )
)
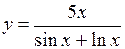 (Ответ:
(Ответ: 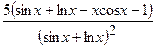 )
)
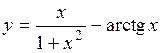 .
(Ответ:
.
(Ответ:  )
)
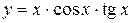 (Ответ:
(Ответ: 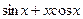 )
)
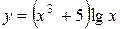 (Ответ:
(Ответ: 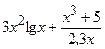 )
)
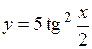 (Ответ:
(Ответ: 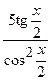 )
)



