при малой выборке. Распределение Стьюдента
Точечная оценка, особенно при малой выборке, может значительно отличаться от истинных параметров генеральной совокупности. При небольшом объеме выборки пользуются интервальными оценками.
В этом случае указывается интервал (доверительный интервал или доверительные границы), в котором с определенной (доверительной) вероятностью  , которую иногда называют «надежностью», находится истинное значение исследуемой или измеряемой величины, например, среднее значение генеральной совокупности.
, которую иногда называют «надежностью», находится истинное значение исследуемой или измеряемой величины, например, среднее значение генеральной совокупности.
Иначе говоря,  определяет вероятность, с которой осуществляются следующие неравенства:
определяет вероятность, с которой осуществляются следующие неравенства:
 ,
,
где положительное число  характеризует точность оценки. Интервал значений от
характеризует точность оценки. Интервал значений от  до
до  называется доверительным интервалом. Разумеется, чем большей надежности мы требуем, тем большим получается доверительный интервал и, наоборот, чем больший доверительный интервал мы задаем, тем вероятнее, что результаты измерений не выйдут за его пределы.
называется доверительным интервалом. Разумеется, чем большей надежности мы требуем, тем большим получается доверительный интервал и, наоборот, чем больший доверительный интервал мы задаем, тем вероятнее, что результаты измерений не выйдут за его пределы.
Сказанное выше относилось к большому числу измерений. При малом числе измерений (условно будем считать, что при n <30) распределение случайных величин носит несколько отличный от закона нормального распределения характер. Это распределение было выявлено в 1908 году английским математиком Госсетом, опубликовавшим работу на эту тему под псевдонимом «Стьюдент» -студент. Естественно, что при данной надежности доверительный интервал при малом числе измерений в серии должен быть шире, чем при большом числе измерений (чем меньше число измерений, тем больше среднее число измерений отличается от математического ожидания) и должен зависеть не только от  , но и от n. Учитывая это, было предложено, в случае небольшого числа измерений, полуширину доверительного интервала (отклонение выборочного среднего от генерального среднего вычислять через S и некоторый параметр
, но и от n. Учитывая это, было предложено, в случае небольшого числа измерений, полуширину доверительного интервала (отклонение выборочного среднего от генерального среднего вычислять через S и некоторый параметр  , который называется коэффициентом Стьюдента и который выбирается по заданным
, который называется коэффициентом Стьюдента и который выбирается по заданным  и n по таблицам (см. табл.1):
и n по таблицам (см. табл.1):
 ,
,
но  тогда
тогда  <
<  .
.
Таблица 1
Значение коэффициента Стьюдента
| n a
| 0.95
| 0.99
| 0.999
| n a
| 0.95
| 0.99
| 0.999
|
|
| 12.706
| 63.657
| 636.619
|
| 2.103
| 2.878
| 3.922
|
|
| 4.303
| 9.925
| 31.598
|
| 2.093
| 2.861
| 3.883
|
|
| 3.182
| 5.841
| 12.941
|
| 2.086
| 2.845
| 3.850
|
|
| 2.776
| 4.604
| 8.610
|
| 2.080
| 2.831
| 3.819
|
|
| 2.571
| 4.032
| 6.859
|
| 2.074
| 2.819
| 3.792
|
|
| 2.447
| 3.707
| 5.950
|
| 2.069
| 2.807
| 3.767
|
|
| 2.365
| 3.499
| 5.405
|
| 2.064
| 2.797
| 3.745
|
|
| 2.306
| 3.355
| 5.041
|
| 2.060
| 2.787
| 3.725
|
|
| 2.262
| 3.250
| 4.781
|
| 2.056
| 2.779
| 3.707
|
|
| 2.228
| 3.169
| 4.587
|
| 2.052
| 2.771
| 3.690
|
|
| 2.201
| 3.106
| 4.487
|
| 2.048
| 2.763
| 3.674
|
|
| 2.179
| 3.055
| 4.318
|
| 2.045
| 2.756
| 3.659
|
|
| 2.160
| 3.012
| 4.221
|
| 2.042
| 2.750
| 3.646
|
|
| 2.145
| 2.977
| 4.140
|
| 2.021
| 2.704
| 3.551
|
|
| 2.131
| 2.947
| 4.073
|
| 2.000
| 2.660
| 3.460
|
|
| 2.120
| 2.921
| 4.015
|
| 1.980
| 2.617
| 3.374
|
|
| 2.110
| 2.898
| 3.965
| ¥
| 1.960
| 2.576
| 3.291
|
Анализ табл. 1 для значений коэффициента Стьюдента показывает, что при числе наблюдений 30 и более (большая выборка) при доверительной вероятности 0,95 он оказывается равным 2, при доверительной вероятности 0,997 - 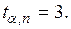 Это означает, что для большой выборки мы опять пришли к нормальному закону распределения или, другими словами, распределение Стьюдента перешло в распределение Гаусса. Приведем (рис.3) график зависимости коэффициента Стьюдента от числа измерений для
Это означает, что для большой выборки мы опять пришли к нормальному закону распределения или, другими словами, распределение Стьюдента перешло в распределение Гаусса. Приведем (рис.3) график зависимости коэффициента Стьюдента от числа измерений для  , который хорошо иллюстрирует только что сделанный вывод. Достаточно хорошо аппроксимировать его можно зависимостью:
, который хорошо иллюстрирует только что сделанный вывод. Достаточно хорошо аппроксимировать его можно зависимостью:
 .
.
Рис. 3

 , которую иногда называют «надежностью», находится истинное значение исследуемой или измеряемой величины, например, среднее значение генеральной совокупности.
, которую иногда называют «надежностью», находится истинное значение исследуемой или измеряемой величины, например, среднее значение генеральной совокупности. ,
, характеризует точность оценки. Интервал значений от
характеризует точность оценки. Интервал значений от  до
до  называется доверительным интервалом. Разумеется, чем большей надежности мы требуем, тем большим получается доверительный интервал и, наоборот, чем больший доверительный интервал мы задаем, тем вероятнее, что результаты измерений не выйдут за его пределы.
называется доверительным интервалом. Разумеется, чем большей надежности мы требуем, тем большим получается доверительный интервал и, наоборот, чем больший доверительный интервал мы задаем, тем вероятнее, что результаты измерений не выйдут за его пределы. , но и от n. Учитывая это, было предложено, в случае небольшого числа измерений, полуширину доверительного интервала (отклонение выборочного среднего от генерального среднего вычислять через S и некоторый параметр
, но и от n. Учитывая это, было предложено, в случае небольшого числа измерений, полуширину доверительного интервала (отклонение выборочного среднего от генерального среднего вычислять через S и некоторый параметр  , который называется коэффициентом Стьюдента и который выбирается по заданным
, который называется коэффициентом Стьюдента и который выбирается по заданным  тогда
тогда  <
<  .
.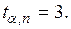 Это означает, что для большой выборки мы опять пришли к нормальному закону распределения или, другими словами, распределение Стьюдента перешло в распределение Гаусса. Приведем (рис.3) график зависимости коэффициента Стьюдента от числа измерений для
Это означает, что для большой выборки мы опять пришли к нормальному закону распределения или, другими словами, распределение Стьюдента перешло в распределение Гаусса. Приведем (рис.3) график зависимости коэффициента Стьюдента от числа измерений для  , который хорошо иллюстрирует только что сделанный вывод. Достаточно хорошо аппроксимировать его можно зависимостью:
, который хорошо иллюстрирует только что сделанный вывод. Достаточно хорошо аппроксимировать его можно зависимостью: .
.



