Элементы регрессионного анализа
После того, как установлено наличие корреляционной связи между двумя изучаемыми признаками (явлениями), можно попытаться установить закономерность зависимости одного признака
Чтобы получить уравнение 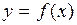 , требуется аппроксимировать (лат. approximare – приближаться) эмпирическую линию регрессии (ЭЛР), которую получают путем соединения точек диаграммы (рис. 10) подходящей теоретической линией регрессии (ТЛР). , требуется аппроксимировать (лат. approximare – приближаться) эмпирическую линию регрессии (ЭЛР), которую получают путем соединения точек диаграммы (рис. 10) подходящей теоретической линией регрессии (ТЛР).
а б Рис. 10 На рис.10 а) показана нелинейная связь между величинами, а на рис.10.б) – линейная. Выше мы говорили о простейшей корреляционной связи – линейной. Поэтому все внимание обратим на рис. 10 б. Для этого случая уравнение связи
Для того чтобы получить конкретное уравнение связи необходимо определить коэффициенты a и b. Определение коэффициентов уравнения ТЛР производится различными способами, самым точным из них является метод наименьших квадратов. Название метода происходит из основного требования замены ЭЛР на ТЛР – аппроксимация будет осуществлена наилучшим образом, если ТЛР наилучшим образом будет приближаться к ЭЛР, в этом случае сумма отклонений значений функции из уравнения ТЛР – yТ от значений функции в эксперименте – yЭ (для одного и того же значения аргумента x) будет минимальной:
Для устранения влияния знака разности берут квадраты:
но
Известно, что если функция в некоторой точке имеет минимум, то производная ее в этой точке равна 0. Поэтому приравниваем нулю производные суммы по параметрам a и b. Полученную систему уравнений решаем относительно a и b. Полученные значения коэффициентов подставляем в уравнение Поиск аппроксимирующего уравнения – это искусство, которым можно овладеть, только в результате накопления большого опыта. На помощь экспериментаторам в настоящее время пришли многочисленные программы для обработки экспериментальных данных. В частности, кривую ТЛР на рис. 10 а) можно описать при помощи уравнения
Конечно, без помощи вычислительной машины и соответствующих программ найти все коэффициенты в этом уравнении довольно трудно. Но вряд ли даже исследователь будет пользоваться этим уравнением: слишком много параметров. Оказывается можно подобрать несколько кривых ТЛР (теоретической линии регрессии). При обработке экспериментальных данных исследователю помогает еще здравый смысл, представление о возможном характере взаимосвязи величин. Все это позволяет выбрать наиболее подходящее уравнение для описания полученных экспериментальных закономерностей. Чаще при обработке эксперимента на начальном этапе исследователь ограничивается графическим проведением ТЛР с учетом метода наименьших квадратов: кривая должна быть плавной и равноотстоять от всех экспериментальных точек.
|

 , являющегося в нашем случае функцией, от другого
, являющегося в нашем случае функцией, от другого  (аргумента). Зная закономерность
(аргумента). Зная закономерность 

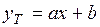 .
.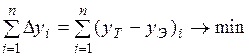 .
. ,
,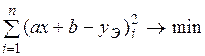 .
.



