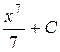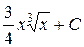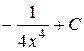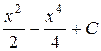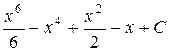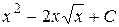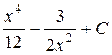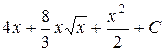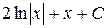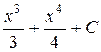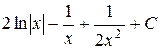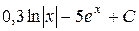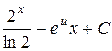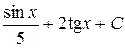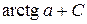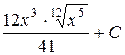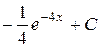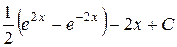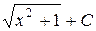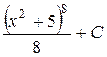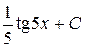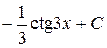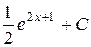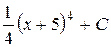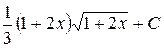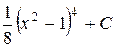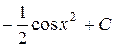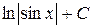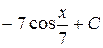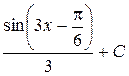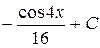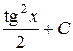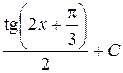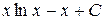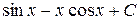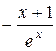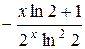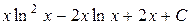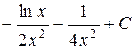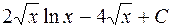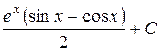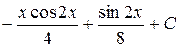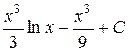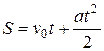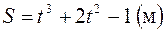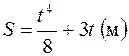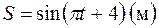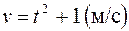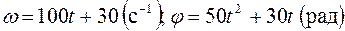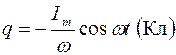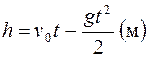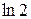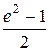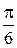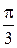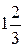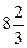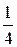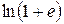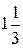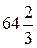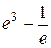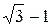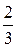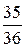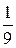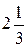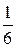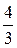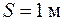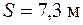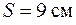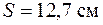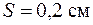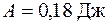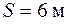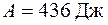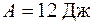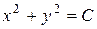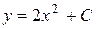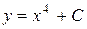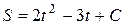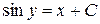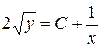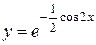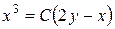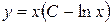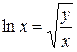П.1.3. Вычисления с приближенными числами.
Точность результата математических операций с приближенными числами определяется количеством значащих цифр в этих числах. Значащими цифрами числа называется число надежно установленных цифр в записи результата измерения. Так в записи 23,21 см мы имеем четыре значащих цифры, а в записи 0,062 см – две. В процессе измерений или в ходе вычислений не следует сохранять в окончательном ответе больше знаков, чем имеется значащих цифр в наименее точно измеренной величине. Результат любого арифметического действия с приближенными числами есть также приближенное число, в котором могут быть и неверные цифры, подлежащие отбрасыванию. Так как сложение и умножение верной цифры и неверной дает неверную, а верной и сомнительной – сомнительную, то результат вычисления, очевидно, не может быть точнее самого неточного числа в исходных данных. Отсюда ясно, что не только окончательные результаты, но и числа в промежуточных выкладках, а также исходные приближенные числа необходимо округлять. Округление надо производить следующим образом. - при сложении и вычитании все слагаемые округляют до сомнительной цифры, стоящей в самом высшем разряде, а затем производят сложение. Пример:
Рот вычитании близки по величине чисел возможно потеря относительной точности. Например, в случае разности
исходные данные имеют по 5 значащих цифр, а результат – две, причем только одну верную цифру. Увеличение точности в таких случаях возможно только путем изменения метода измерений (или вычислений) и, следовательно, использования расчетной формулы, не содержащей разности близких величин; - при умножении и делении в полученном результате будет столько значащих цифр, сколько в исходном данном с наименьшим количеством значащих цифр. Аналогично предыдущему следует предварительно округлять все числа, оставляя, если это может повлиять на результат, одну запасную цифру. Пример: - при возведении в степень и извлечении корня приближенного числа должно быть оставлено значащих цифр столько, сколько их в основании. Пример: В числе, полученном после извлечения корня любой степени, следует оставлять столько значащих цифр, сколько их было в числе под корнем. Пример: - при логарифмировании в мантиссе приближенного числа берется столько значащих цифр, сколько их в логарифмируемом числе. Пример:
Вычисление погрешности измерений производят с такой же точность, что и вычисление самой измеряемой величины, а это означает, что при записи погрешности в ней будет столько же десятичных знаков, сколько их в записи самого результат. На погрешность правило значащих цифр не распространяется. Например: Правильно. Неправильно. Z= 284 Z= 52,7 Z= 4,750 ОТВЕТЫ
Глава 4
Глава 5
СПИСОК ЛИТЕРАТУРЫ
Герасимов А.Н.. Медицинская статистика: учебное пособие / А.Н. Герасимов- М.: МИА, 2007.-475с. Кучеренко В.З.. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие для медицинских вузов / В.З. Кучеренко. - М.: ГЭОТАР- Медиа, 2007.-245с. Павлушков И.В. Основы высшей математики с математической статистикой: учебник для мед. и фармац. вузов / И.В.Павлушков. -изд. 2-е исправ.- М.: ГЭОТАР- Медиа, 2007.-422с. Ремизов А.Н. Курс лекций: учебник / А.Н.Ремизов, А.Я. Потапенков - изд. 3-е..- М.: Дрофа, 2006.-720с.. Чернов В.И.. Математическая статистика с основами высшей математики: учебник / В.И. Чернов и др. - Воронеж: ГОУ «Воронеж. гос. мед. акад. им Н.Н Бурденко», 2006.-317с.
Учебное издание Методические разработки к практическим занятиям по высшей математике и математической статистике
|

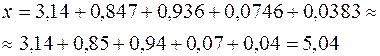
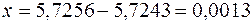
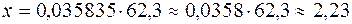 ;
;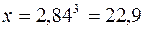 .
. ;
;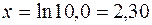 .
.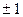 Z= 284,5
Z= 284,5 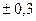 Z= 52.74
Z= 52.74 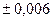 Z= 4,75
Z= 4,75