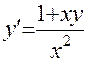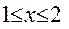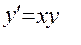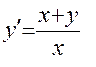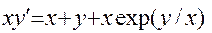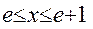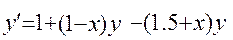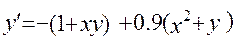Задание на работу .

Решить задачу Коши на равномерной сетке. Решение найти в четырех узловых точках

(шаг h₁ равен [ b - a ] / 4). Найти решение в тех же узлах, ведя расчет с уменьшенным вдвое шагом. Вычислить погрешности приближений при расчете с шагом h₂ = h₁ / 2

Задачу решить с помощью системы MATHCAD:

а) методом Эйлера;

б) методом Эйлера - Коши;

в) методом Рунге - Кутта.

 

Варианты лабораторных работ.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

Вспомогательные материалы.

 

Пример

Решить задачу Коши

на равномерной сетке с шагом h = 0.1. Решение найти в четырех узловых точках.

С помощью программы найти решение в тех же узлах, ведя расчет с уменьшенным вдвое шагом. Вычислить погрешности приближений при расчете с шагом h = 0.05

Задачу решить:

а) методом Эйлера;

б) методом Эйлера - Коши;

в) методом Рунге - Кутта.

 

Решение. Здесь f (x,y) = x + y; m = 4; a = 0; b = 0.4;

h = (b - a) / m = 0.4 /4 = 0.1

а) Используя рекуррентные формулы

x₀ = 0; y₀ = 1; x_i = x _{i - 1} + 0.1; y _i = y _{i - 1} + 0.1(x _{i - 1} + y _{i - 1}) i = (1, 2, 3, 4),

последовательно находим

при i = 1: x₁ = 0.1; y₁ = 1 + 0.1(0 + 1) = 1.1;

при i = 2; x₂ = 0.2; y₂ = 1.1 + 0.1(0.1 + 1.1) = 1.22;

при i = 3; x₃ = 0.3; y₃ = 1.22 + 0.1(0.2 + 1.22) = 1.362;

при i = 4; x₄ = 0.4; y₄ = 1.362 + 0.1(0.3 + 1.362) = 1.5282.

С помощью программы находим решение при h = 0.05.

Обозначив, d _i = | y _i (h) - y _i (h/2) | сведем результаты вычислений в таблицу

 

I	x i	y i (h)	y i (h / 2)	d
	0.1	1.1	1.105	0.005
	0.2	1.22	1.231012	0.011012
	0.3	1.362	1.380119	0.018191
	0.4	1.5282	1.554911	0.028738

б) Формулы (7) в нашем случае принимают вид

 

k₁^{[ i - 1]} = h (x_i-1 + y_i-1), k₂^{[ i - 1 ]} = h (x_i-1 + h + y_i-1 + k₁^{[ i - 1]})

x_i =x_i-1 + h, y_i = y_i-1 + (1/2)[ k₁^{[i -1]} + k₂^{[i -1]}] (i = 1, 2, 3, 4).

 

Полагая x ₀ = 0, y ₀ = 1, последовательно находим

 

при i = 1:

 

k₁^{[ 0 ]} =0.1(0 + 1) = 0.1; k₂^{[ 0 ]} = 0.1(0 + 0.1 + 1 + 0.1) = 0.12;

x₁= 0 + 0.1 = 0.1; y₁ = 1 + (1/2)(0.1 + 0.12) = 1.11;

 

при i = 2:

 

k₁^{[ 1 ]} =0.1(0.1 + 1.11) = 0.121; k₂^{[ 1 ]} = 0.1(0.1+0.1+1.11+0.121) = 0.1431;

x₁= 0.1 + 0.1 = 0.2; y₁ = 1.11+(1/2)(0.121+0.143) = 1.2425.

 

Далее получаем при i = 3: x ₃ = 0.3_; y ₃ = 1.398465;

При i = 4: x ₄ = 0.4_; y ₄ = 1.581804.

С помощью программы проводим вычисления с половинным шагом. Результаты заносим в таблицу, аналогичную таблице пункта а).

 

в) Из формул (8) получаем

 

k₁^{[ i - 1]} = h (x_i-1 + y_i-1), k₂^{[ i - 1 ]} = h (x_i-1 + (1/2)h + y_i-1 +(1/2) k₁^{[ i - 1]})

k₃^{[ i - 1 ]} = h (x_i-1 + (1/2)h + y_i-1 +(1/2) k₂^{[ i - 1]})

k₄^{[ i - 1 ]} = h (x_i-1 + h + y_i-1 + k₃^{[ i - 1]})

x_i =x_i-1 + h, y_i = y_i-1 + (1/6)[ k₁^{[i -1]} + 2k₂^{[i -1]} + 2k₃^{[i -1]} + k₄^{[ i - 1 ]}]

для i = 1, 2, 3, 4.

 

Полагая x ₀ = 0, y ₀ = 1, последовательно находим

 

при i = 1:

 

k₁^{[ 0 ]} =0.1(0 + 1) = 0.1; k₂^{[ 0 ]} = 0.1(0 + 0.05 + 1 + 0.05) = 0.11;

k₃^{[ 0 ]} = 0.1(0 + 0.05 + 1 + 0.055) = 0.1105

k₄^{[ 0 ]} = 0.1(0 + 0.1 + 1 + 0.1105) = 0.121050

x₁= 0 + 0.1 = 0.1; y₁ = 1 +(1/6)(0.1 + 2*0.11+2*0.1105+

+0.12105) = 1.110342;

при i = 2:

 

k₁^{[ 1 ]} =0.1(0.1 + 1.110342) = 0.1210342;

k₂^{[ 1 ]} = 0.1(0.1 + 0.05 + 1.110342 + 0.0605171) = 0.1326385;

k₃^{[ 1 ]} = 0.1(0.1 + 0.05 + 1.110342 + 0.06604295) = 0.1326385;

k₄^{[ 1 ]} = 0.1(0.1 + 0.1 + 1.110342 + 0.1326385) = 0.1442980.

x₂= 0.1 + 0.1 = 0.2;

y₂ = y₁ +(1/6) [ k₁^[1] + 2 k₂^[1] +2 k₃^[1] + k₄^[1]] = 1.242805;

 

Далее получаем при i = 3 x₃ = 0.3; y₃ = 1.399717;

i = 4 x₄ = 0.4; y₄ = 1.583648;

 

С помощью программы проводим вычисления с половинным шагом. Результаты заносим в таблицу.

 

2. Блок - схема численного решения задачи Коши для дифференциального уравнения первого порядка методами Эйлера, Эйлера - Коши и Рунге - Кутта

 

Методом   Рунге -   Кутта

Методом   Эйлера -   Коши

Методом Эйлера

Вычисление приближенного решения на одном шаге

 

3. Пример программы для функции y ^/ = x + y

(пример приведен для удобства разработки программы на MATHCADе студентами, привыкшими работать в ПАСКАЛЕ))

program DifEquationsFirstOrder;

{*******************************************************}

uses Crt;

const

c:array[1..4] of real = (0,0.5,0.5,1);

type

coef = array[0..4] of real;

var

i,j,m:integer;

a,b,h,x,y,y1,y2,y3:real;

k0,k:coef;

ch:char;

{-----------------------SUBROUTINES---------------------}

{ Y = F (x,y) (f = x+y) }

function f(x,y:real):real;

BEGIN

f:= x + y

END;

{-------------------------------------------------------}

procedure Pausa;

BEGIN

WRITELN;WRITELN ('Для продолжения нажмите любую клавишу...');

REPEAT ch:= readkey UNTIL ch <> '';

END;

{------------------ОСНОВНАЯ ПРОГРАММА-------------------}

BEGIN

ClrScr;

WRITELN ('Введите значения концов отрезка [a,b]');

READ (a,b);

WRITELN ('Введите начальное значение функции y0 при x=x0 ');

READ (y);

WRITELN (' Введите число значений функции на промежутке [a,b]');

READ (m);

x:= a; h:= (b-a) / m; y1:= y; y2:= y; y3:=y;

WRITELN (' Метод Эйлера Метод Э.-Коши Метод Р.-Кутта');

WRITELN ('x=',x:5:2,' y1=',y:9:6,' y2=',y2:9:6,' y3=',y3:9:6);

FOR i:= 1 TO m DO

BEGIN

y1:= y1 + h*f(x,y1);

FOR j:=1 TO 2 DO

k0[j]:=h*f(x+2*c[j]*h, y2+2*c[j]*k0[j-1]);

y2:= y2+(k0[1]+k0[2]) / 2;

FOR j:=1 TO 4 DO

k[j]:= h*f(x+c[j]*h, y3+ c[j]*k[j-1]);

y3:= Y3+ (k[1]+2*k[2]+2*k[3]+k[4]) / 6;

x:= x+h;

WRITELN ('x=',x:5:2,' y1=',y1:9:6,' y2=',y2:9:6,' y3=',y3:9:6);

END;

PAUSA;

END.