Мнимая карусель

(Таня – Нулику)

 

Вот тебе, Нулик, наши последние новости.

По дороге к аттракциону все чаще мелькали рекламные плакаты:

ПЕРВАЯ В МИРЕ МНИМАЯ КАРУСЕЛЬ!

ИСКЛЮЧИТЕЛЬНО ДЛЯ МНИМЫХ ЕДИНИЦ!

ЕДИНСТВЕННОЕ МЕСТО,

ГДЕ МНИМЫЕ ЕДИНИЦЫ МОГУТ СТАТЬ

ДЕЙСТВИТЕЛЬНЫМИ!

Мнимые Единицы, кружитесь на здоровье!

Наша симпатичная подружка щебетала без умолку и рассказала кучу интересного.

Оказывается, Мнимая Единица – это просто‑напросто корень квадратный из отрицательной единицы: √–1.

– А разве из минус единицы нельзя извлечь корень? – спросил Сева. – Ведь корень квадратный из единицы всегда равен единице.

– Ой‑ой‑ой! – ужаснулась Мнимая Единичка. – Это касается только положительной единицы. Ведь что значит извлечь корень квадратный, скажем, из девяти?

– Это значит найти такое число, которое при возведении в квадрат равнялось бы девяти, – ответил Олег. – Это число три.

– Верно. А теперь попробуйте найти число, которое при возведении в квадрат дает минус единицу!

Мнимая Единичка тоненько засмеялась.

Сева озадаченно взъерошил волосы:

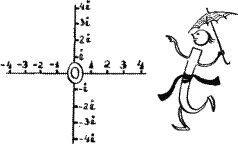
– М‑да! Такого числа нет. Какое число ни возводи в квадрат, положительное или отрицательное, ответ все равно получится положительный. Уж я‑то знаю!

– Вот видите. Потому‑то корень квадратный из минус единицы называется мнимой единицей.

– Выходит, мнимые единицы совсем особые числа. Наверное, и дорога у вас устроена как‑нибудь особенно.

– Ничуть. Наша дорога очень похожа на ту, где живут действительные числа, только расположена она под прямым углом к ней. Это такая же бесконечная прямая, в центре которой находится все та же Нулевая станция.

– Раз у вас есть Нулевая станция, значит есть положительные и отрицательные числа?

– Что вы! Разве мнимые числа могут быть положительными и отрицательными? Просто на нашей дороге, так же как и на дороге действительных чисел, есть два направления от нуля. Одно из них условились обозначать знаком плюс, другое – знаком минус.

– Но как же мнимые числа отличают от действительных?

– С помощью буквы i: 2i, 5i, –8i, –12i.

– Вот как! У вас, как и у других букв в Аль‑Джебре, тоже есть коэффициенты?

– Конечно.

– А где же ваш коэффициент? – ляпнул Сева.

И когда только он научится вести себя в обществе? Хорошо еще, воспитанная Единичка сделала вид, что не заметила его бестактности.

– Мой коэффициент – единица, и он, как всегда, невидимка.

Но Сева уже закусил удила. Ужасный он спорщик!

– Вот вы говорите, что мнимая монорельсовая дорога похожа на действительную. Значит, и правила движения на ней те же. Так ведь? Тогда при чем здесь карусель? Ведь на обычной монорельсовой дороге движение идет по прямой, а карусель‑то кружится?

– Вы отчасти правы, – ответила Мнимая Единичка. – Правила движений у нас более разнообразны. При сложении и вычитании вагончики на мнимой дороге движутся по прямой и по тем же правилам, что и действительные числа; 2i + 3i = 5i; 8i – 15i = – 7i, или вот еще: –3i + 9i = 6i, ну и конечно: 5i – 5i = 0.

Мнимые Единички с разными знаками и одинаковыми коэффициентами взаимоуничтожаются на Нулевой станции.

Иное дело – умножение, деление, возведение в степень… Тут уж Мнимые Единицы двигаются не только по прямой, но и по кривой. Именно это вы сейчас и увидите.

Мы вошли в круглый павильон. Там было полным‑полно Мнимых Единиц. Все они с нетерпением ждали своей очереди покружиться.

Павильон очень похож на цирк. Места расположены амфитеатром. В центре – арена, ее под прямым углом друг к другу пересекают две перекладины. Одна перекладина изображает монорельсовую дорогу действительных чисел. На концах ее укреплены таблички +1 и –1. Другая перекладина изображает дорогу мнимых чисел. Здесь на концах находятся таблички +i и –i. На пересечении дорог, в центре арены, – Нулевая станция. Здесь укреплена вращающаяся ось, и на нее (совсем как патефонная пластинка) надет прозрачный пластмассовый круг.

Когда мы вошли, карусель только что остановилась. С нее легко соскочила Мнимая Единица с зеленым зонтиком. Вместо нее на круг, точно против таблички +i, стала Мнимая Единица с желтым зонтиком.

Наша спутница подошла к микрофону и скомандовала:

– К возведению в степень приготовиться!

Прозвенел звонок, и под звуки плавного вальса круг тронулся. Только не по часовой стрелке, а в обратную сторону. И тут‑то начались необыкновенные вещи!

Мнимая Единица с желтым зонтиком пересекла дорогу действительных чисел у таблички –1 и превратилась в действительное число – Отрицательную Единицу.

Возле таблички снова стала Мнимой Единицей, но уже со знаком минус. Вот она снова пересекла действительную дорогу, поравнялась с табличкой +1 и – невероятно! – опять превратилась из Мнимой Единицы в Действительную, да еще положительную. А потом как ни в чем не бывало возвратилась к табличке i. Тут она снова стала Мнимой.

Оркестр заиграл песню «Каким ты был, таким остался!», и все началось сначала. Карусель кружилась, а Мнимая Единица все превращалась и превращалась.

– Не понимаю, – сказал Сева. – Мнимая Единица превращается в Действительную, Действительная – опять в Мнимую… Как это?

– На то и возведение в степень! – отозвалась Мнимая Единичка. – Ведь Мнимая Единица равняется корню квадратному из минус единицы: i = √–1. Но если возвести в квадрат корень квадратный из любого числа, что получится?

– Подкоренное число, – ответил Олег.

– Так это же мы недавно видели! – вспомнил Сева. – Один карликан целый час возводил в квадрат то корень квадратный из трех, то корень квадратный из двух… И каждый раз получалось число, стоящее под радикалом.

– То же самое происходит и с Мнимой Единицей: i = i * i = (√–1) = –1.

– Ну, это понятно. А как же действительное число – минус единица превращается в мнимое?

– При этом Мнимая Единица возводится уже не в квадрат, а в куб, то есть в третью степень: i = i* i.

А это ведь все равно что умножить минус единицу на i: –1 * i = –i.

– Теперь, – сказал Олег, – нетрудно понять, как Мнимая Единица с минусом –i превращается в Действительную Единицу со знаком плюс +1. Она возводится в четвертую степень: i = i * i

А это можно представить себе и так: –1 * –1 = +1.

– Прекрасно! – воскликнула Мнимая Единичка. – Остается выяснить, как Действительная Единица снова становится Мнимой.

В самом деле, как? Тут даже Олег ни до чего не додумался. Но оказалось, что для этого Мнимую Единицу надо возвести в пятую степень.

– Не может быть! i равно i?! – растерялись мы. – Что же это такое?

– Да ничего особенного: i = 1. Чтобы получить i, умножим единицу на i. А это ведь все равно что i, взятое один раз, то есть просто i: 1 * i = i.

– Вот так история! Мнимую Единицу нельзя возвести более чем в четвертую степень? – удивился Олег.

– Отчего же! – возразила Мнимая Единичка. – Возводите себе на здоровье и в шестую, и в седьмую, и в сто двадцать первую… Словом, в любую целую степень. Но ничего, кроме того, что уже было, не получится. На то и карусель!

Тут Севе срочно понадобилось выяснить, чему равняется i?

– Ну, это совсем нетрудно, i в пятой равно i, – сказала Мнимая Единичка. – Значит, i в девятой тоже равно i…

– Понимаю! – перебил Сева. – Каждый раз надо прибавлять к показателю степени четыре: i равно i, значит, i тоже равно 1.

Вот, Нулик, хорошая задача для твоих учеников. Попробуйте вычислить, чему равно i? А чтобы вам легче было, загляните в чертеж мнимой карусели.

Долго еще любовались мы превращениями Мнимых Единиц, а когда уже собрались уходить, Сева хлопнул себя по лбу:

– Чуть не забыл спросить! Вы сказали, что при возведении в степень Мнимые Единицы движутся по кривой. А ведь здесь они движутся по окружности!

– Окружность тоже кривая, но такая, где все точки находятся на одинаковом расстоянии от центра. При умножении и возведении в степень перемещаются по окружности только Мнимые Единицы.

– А как движутся другие мнимые числа при возведении в степень? – спросил Олег. – Два i, три i, четыре i?

– На нашей карусели вы этого не увидите, – сказала Мнимая Единичка. – Да оно и к лучшему. Это очень сложный вопрос. Нельзя же все сразу…

– Всякому овощу свое время? – подмигнул Сева.

– Пожалуй, – улыбнулась Мнимая Единичка.

Мы поблагодарили ее и распрощались. Но тут пришла очередь Олегу хлопать себя по лбу.

– Извините, пожалуйста, – сказал он, обернувшись, – а зачем вообще нужны мнимые числа?

– Это вы поймете, когда начнете решать уравнения второй и третьей степени. Там в ответе часто получаются мнимые числа.

– На что нужны уравнения с мнимыми ответами? – буркнул Сева.

– Спросите об этом у физиков, химиков, инженеров, астрономов… Мнимые числа помогают им решать вовсе не мнимые, а действительно важные практические задачи.

– Но почему же тогда вас называют мнимыми?

– По привычке, – грустно ответила буковка i. – Так нас окрестил французский ученый Рене Декарт. Это было в семнадцатом веке, когда мнимые числа ни во что не ставились. Но с тех пор многое переменилось. Если бы Декарт жил в наши дни, он непременно придумал бы для нас более подходящее название.

– Например, «необходимые числа», – сказал Олег.

– О! Это было бы чудесно! – вздохнула Мнимая Единичка.

Мы еще раз попрощались и ушли. На этот раз совсем.

Таня.