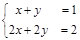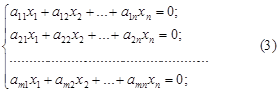Крамер формуласы

 

Баяндауымызды жеңілдету үшін үшінші ретті алгебралық сызықтық теңдеулер жүйесін қарастыралық:

Мынандай анықтауыштар есептелген болсын:

Δ; анықтауышы (1) жүйенің анықтауышы деп аталынады. Ал Δ_x, Δ_y, Δ_z анықтауыштары Δ; анықтауышының сәйкес бірінші, екінші, үшінші бағандарын бос мүшелермен ауыстырудан алынған анықтауыштар.

Мынандай жағдайлар болуы мүмкін:

1. (Δ≠0). Бұл кезде жүйенің жалғыз ғана шешімі бар, ол шешім мына формулалармен анықталады:

Бұл формулалар Крамер формулалары деп аталынады.

2. (Δ=0). Мұндай кезде жүйенің шешімі болмауы да немесе шексіз көп шешімдері болуы да мүмкін. Мысалы

жүйесінің шешімі жоқ, ал

жүйесінің шексіз көп шешімі бар.

 

Біртектес сызықтық алгебралық теңдеулер жүйесі

 

Сызықтық алгебралық теңдеулер жүйесіндегі барлық бос мүшелер нольге тең болатын болса, ондай теңдеуді біртектес сызықтық алгебралық теңдеулер жүйесі деп айтамыз:

Біртектес сызықтық алгебралық теңдеулер жүйесі барлық уақытта үйлесімді (r(A)=r(Ā)), оның барлық уақытта нольдік шешімі бар: x₁=x₂=…x_n=0.

Теорема 1. (3) жүйенің нольден ерекше шешімдері бар болуы үшін жүйенің матрицасының рангісі белгісіздер санынан кіші болуы қажетті және жеткілікті, яғни r(A)<n.

Теорема 2. n теңдеуден тұратын n белгісізі бар біртектес сызықтық алгебралық теңдеулер жүйесінің нольден ерекше шешімдері бар болуы үшін жүйенің анықтауышының нольге тең болуы қажетті және жеткілікті.