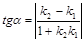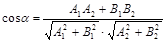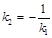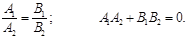Түзудің жалпы теңдеуі
Ax+By+С=0 (1) Мұнда A, B, C тұрақты коэффициенттер, олар A2+B2≠0 шартын қанағаттандыруы керек. Егер осы коэффициенттердің бірі нольге тең болса, онда түзудің толық емес жалпы теңдеуін аламыз. · Егер А=0 болса, онда By+C=0 теңдеуі Ох осіне параллель түзу теңдеуі болады. · Егер В=0 болса, онда Ax+C=0 теңдеуі Оу осіне параллель түзуді анықтайды. · Егер С=0 болса, онда Ax+By=0 теңдеуі анықтап тұрған түзу координаталар системасының бас нүктесі арқылы өтеді. · Егер А=С=0 болса, онда By=0 теңдеуі Ох осінің теңдеуі болады. · Егер В=С=0 болса, онда Ах=0 теңдеуі Оу осінің теңдеуі болады. Екі түзу қиылысуы мүмкін, немесе олар өзара параллель болуы мүмкін. Екі түзу тік бұрыш жасап қиылысатын болса, онда олар өзара перпендикуляр болады. Егер екі түзу y=k1x+b1, y=k2x+b2 теңдеулері арқылы беріліп тұрса, олардың арасындағы сүйір бұрыш мына формуламен есептеледі:
Ал егер екі түзу А1х+В1у+С1=0, А2х+В2у+С2=0 жалпы теңдеулерімен берілсе, олардың арасындағы бұрышты мына формуламен есептеуге болады:
Түзулер бұрыштық коэффициентпен өрнектелген теңдеулері арқылы берілсін. Егер олар өзара параллель болса, онда tgα=0, сондықтан k2=k1 (түзулердің өзара параллель болу шарты). Түзулердің өзара перпендикуляр болу шарты төмендегідей болады:
Егер түзулер жалпы теңдеулері арқылы берілсе, онда олардың өзара параллель, өзара перпендикуляр болу шарттарын сәйкес былай жазуға болады:
|