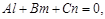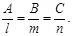Кеңістіктегі түзулер. Кеңістікте түзу мен жазықтықтың өзара орналасуы
Кеңістікте түзуді екі жазықтықтың қиылысу сызығы деп қарауға болады, сондықтан осы екі жазықтықтың теңдеулерінен тұратын жүйені түзудің кеңістіктегі теңдеуі есебінде қарастыруға болады.
(1) жүйені теңдеудің жалпы теңдеуі деп атайды. Нақты есептерді шешкен кездерде түзудің теңдеуін (1) қолдану кейде едәуір ыңғайсыздық тудырады. Сондықтан ондай кездерде түзудің басқа түрде берілген теңдеулерін пайдаланады. Бізге L түзуі мен нольден ерекше a {l,m,n} векторы берілсін, бұл вектор түзуде жатсын, немесе оған параллель болсын. L түзуінің бойынан M(x1,y1,z1) нүктесін алалық. Онда қарастырып отырған түзудің теңдеуін мына түрде жазуға болады:
Бұл теңдеуді түзудің канондық теңдеуі деп атайды. t параметрін енгізу арқылы канондық теңдеуден түзудің параметрлік теңдеуін алуға болады:
Бізге екі түзу өздерінің канондық теңдеулері арқылы берілсін:
Осы екі түзу құрап тұрған бұрыштардың бірі a1 {l1,m1,n1}, a2 {l2,m2,n2} векторларының арасындағы ϕ =(a 1^ a 2) бұрышқа тең болады. Ол бұрышты мына формула арқылы есептеуге болады:
Кеңістіктегі екі түзудің сәйкес параллель немесе перпендикуляр болу белгісі мынадай болады:
Енді
Түзу мен жазықтықтың сәйкес параллельдік, перпендикулярлық белгілері мынандай болады:
|
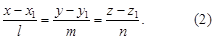
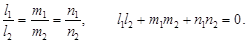
түзуі мен Ax+By+Cz+D=0 жазықтығының өзара орналасуын қарастыралық. Олардың арасындағы бұрыш былай анықталады:
