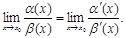Тамаша шектер. Ақырсыз аз функцияларды салыстыру
Төмендегідей екі шек өте жиі кездесетін шектер:
Бұларды бірінші және екінші тамаша шектер деп атайды.
Екінші тамаша шекті e саны деп атайды (әйгілі математик Эйлердің құрметіне). Бұл сан иррационал сан болады, тек қана иррационал сан емес әрі трансцендентті сан (коэффициенттері бүтін сан болатын көпмүшеліктің түбірі болмайтын сан) болады. Негізі e саны болатвын логарифмді натурал логарифм деп атайды, ал осы натурал логарифмдік функцияны y=lnx деп белгілейді (ондық логарифмдік функция y=lgx деп белгіленетінін мектем курсынан білеміз). Егер
яғни кез-келген ε>0 саны үшін δ>0 саны табылып 0<|x-x0|<δ; болған кезде |α(x)|<ε; орындалатын болса, онда α(x) функциясын х→x0 да ақырсыз аз функция, немесе ақырсыз аз шама деп атаймыз. Ақырсыз α(x), β(x) (х→x0) аз шамалар нольге әртүрлі жылдамдықтармен ұмтылуы мүмкін. Кей жағдайларда олардың нольге ұмтылу жылдамдықтарын салыстыруға тура келеді. Екі α(x), β(x) (х→x0) ақырсыз аз шамалардың нольге ұмтылу жылдамдықтарын салыстыру үшін олардың х→x0 да қатынасының шегін табады:
Егер С≠0 болса, онда α(x), β(x) ақырсыз аз шамаларының ақырсыз аздық реттері бірдей (нольге ұмтылу жылдамдықтары бірдей) деп айтады. Егер С=0 болса, онда α(x) шамасының ақырсыз аздығы β(x) шамасымен салыстырғанда жоғары деп, ал β(x) шамасының α(x) мен салыстырғанда ақырсыз аздығы төмен деп айтады. Егер
болса, онда α(x) шамасының ақырсыз аздық реті β(x) шамасымен салыстырғанда k болады деп айтады. Егер
болса, онда α(x), β(x) (х→x0) шамаларын эквивалентті шамалар деп айтып α(x)≈β(x) деп белгілейді. Теорема 3. Егер α(x)≈α’(x), х→x0 және β(x)≈β’(x), х→x0 болса, онда х→x0 да төмендегі теңдік орындалады:
|