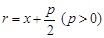Екінші ретті қисықтар
Анықтама 1. Центр деп аталатын нүктеден бірдей қашықтықта орналасқан нүктелер жиынын шеңбер деп атайды. Шеңбер нүктелерінің центрден ара қашықтығын шеңбердің радиусы деп атайды. Радиусы R, центрі O(a;b) нүктесінде орналасқан шеңбердің канондық теңдеуі былай жазылады:
Анықтама 2. Фокус деп аталатын екі берілген нүктелерден ара қашықтықтарының қосындысы тұрақты сан (2а) болатын (ол сан фокустардың ара қашықтығы болатын 2с санынан үлкен) нүктелер жиынын эллипс деп атайды. Эллипстің канондық теңдеуі мынадай болады:
Егер a=b болса, онда эллипс радиусы a болатын, центрі координаталар системасының бас нүктесінде жататын шеңберге айналады. Эллипстің формасын эксцентриситет деп аталатын төмендегі шама сипаттайды:
Эллипсте жатқан нүктенің фокустардан ара қашықтығы эллипстің фокалдық радиустары деп аталады. Фокалдық радиустар мына формуламен есептеледі:
мұнда сол жақтағы фокалдық радиус-вектор үшін «+» таңбасы, ал оң жақтағы фокалдық радиус-вектор үшін «-» таңба алынады. Анықтама 3. Фокустар деп аталатын екі нүктеден ара қашықтықтарының айырымы тұрақты санға (2а - саны, бұл сан фокустардың ара қашықтығы 2с санынан кіші болуы керек) тең болатын нүктелер жиынын гипербола деп атайды. Гиперболаның канондық теңдеуі:
мұнда b2=c2-a2. c- саны фокустардың ара қашықтығының жартысына тең. a, b сандары гиперболаның нақты және жорамал жарты осьтері деп аталады. Гиперболаның формасын оның эксцентриситеті сипаттайды:
Гиперболада жатқан нүктесінен фокустарға дейінгі ара қашықтық фокальдық радиустар деп аталады. Олар мына формуламен есептеледі:
мұнда сол жақтағы фокалдық радиус-вектор үшін «+» таңбасы, ал оң жақтағы фокалдық радиус-вектор үшін «-» таңба алынады. Егер a=b болса, онда
гипербола теңбүйірлі гипербола деп аталынады. Мына теңдеулермен анықталатын гиперболалар
түйіндес гиперболалар деп аталады.
Егер параболаның директрисасының теңдеуі x=-p/2 болса, ал оның фокусы F(p/2;0) нүктесі болса, параболаның теңдеуі мынандай болады: y2=2px Бұл парабола абсцисса осіне қарағанда симметриялы болады. Фокалдық радиус-вектордың ұзындығы
формуласымен есептеледі: x2=2py теңдеуі де параболаның теңдеуі болады, бұл парабола ординаталар осіне қарағанда симметриялы орналасқан.
|


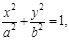
 мұнда b2=a2-c2. с- саны фокустардың ара қашықтығының жартысына тең. a, b сандары эллипстің үлкен және кіші жарты осьтері деп аталады.
мұнда b2=a2-c2. с- саны фокустардың ара қашықтығының жартысына тең. a, b сандары эллипстің үлкен және кіші жарты осьтері деп аталады.




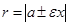


 Анықтама 4. Фокус деп аталатын нүкте мен директрис а деп аталатын түзуден қашықтықтары өзара тең болатын нүктелер жиыны парабола деп аталады.
Анықтама 4. Фокус деп аталатын нүкте мен директрис а деп аталатын түзуден қашықтықтары өзара тең болатын нүктелер жиыны парабола деп аталады.