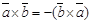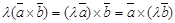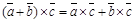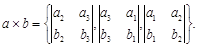Анықтама 2. a векторына қосқанда қосындысы b болатын векторды b мен a векторының айырмасы деп атаймыз да былай белгілейміз b-a.
Егер a {a1,a2,a3}, b {b1,b2,b3} болса, онда b-a ={b1-a1, b2-a2, b3-a3} болады. Анықтама 3. a векторы мен λ; санының көбейтіндісі деп ұзындығы |λ|| a | болатын, ал бағыты λ>0 болса a векторының бағытымен бірдей болатын; ал λ<0 болса бағыты a векторына қарама қарсы болатын векторды айтады. Ол вектор λ a арқылы белгіленеді. Егер a {a1,a2,a3} болса, онда λ a ={λa1,λa2,λa3} болады. Анықтама 4. Екі нольден ерекше a,b векторларының скалярлық көбейтіндісі деп олардың ұзындықтары мен екеуінің арасындағы бұрыштың косинусының көбейтіндісін айтады да (ab) деп белгілейді, яғни: ( ab )=| a || b |cos(a^b). Егер a {a1,a2,a3}, b {b1,b2,b3} болса, онда ( ab )=a1b1+a2b2+a3b3 болады. Скалярлық көбейтіндінің қасиеттері: 1. (ab)=(ba); 2. ((λ a) b) =λ(ab); 3. (a (b + c))=(ab)+(ac); 4. (aa)= a 2=| a |2; 5. (a ^ b)=900→(ab)=0; 6. cos(a ^ b)=(ab)/(| a || b |) 7. Егер векторлардың координаталары пропорционал болатын болса, олардың бағыттары параллель (коллинеар) болады
1. a, b векторларының әрқайсысына перпендикуляр; 2. ұзындығы | a || b |sin(a ^ b) болады; 3. c векторының соңынан қарағанда a векторынан b векторына қысқа жолмен бұрылу сағат тіліне қарсы бағытта болады. Векторлық көбейтінді [ a,b ] болмаса a x b деп белгіленеді. Векторлық көбейтіндінің геометриялық мағынасы. Векторлық көбейтіндінің нәтиежесінде алынатын вектордың ұзындығы көбейткіш векторлар қабырғалары болатын параллелограммның ауданына тең болады. Векторлық көбейтіндінің қасиеттері: 1. 2. 3. 4. Егер a {a1,a2,a3}, b {b1,b2,b3} болса, онда
|

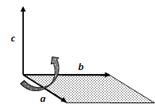 Анықтама 5. Екі a, b вектордың векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын c векторын айтады:
Анықтама 5. Екі a, b вектордың векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын c векторын айтады: