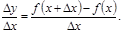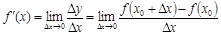Туындының анықтамасы

Бір аралықта (кесіндіде, интервалда) анықталған y=f(x) функциясы берілсін. Егер x нүктесінде аргумент Δx өсімше қабылдайтын болса, осы нүктеде функция да өсімше қабылдайды. Сонымен аргументтің x мәнінде функция мәні y=f(x) болады, ал аргуметтің x+Δx мәнінде функцияның мәні y+Δy=f(x+Δx) болады. Онда функцияның x нүктесіндегі өсімшесі Δy=f(x+Δx)-f(x) болады. Енді функция өсімшесінің аргумент өсімшесіне қатынасын қарастыралық:

Енді Δx→0 болғанда осы қатынастың шегі бар болсын делік, ол шекті f’(x) деп белгілеп f(x) функциясының x нүктесіндегі туындысы деп атаймыз. Сонымен анықтама бойынша:

немесе

Сонымен y функциясының x аргументі бойынша туындысы деп аргумент өсімшесі нольге ұмтылғанда функция өсімшесінің аргумент өсімшесіне қатынасының шегі бар болса сол шекті айтамыз екен.

Жалпы жағдайда функцияның кез-келген x нүктесінде оның туындысы f’(x) бар болады, сондықтан туындының өзі x аргументінің функциясы болады екен.

Туындыны оқулықтарда әртүрлі қылып белгілейді, мысалы:

Кейде туындының x=a нүктесінде есептелгенін көрсету керек болса мынандай да белгілеу қолданылады: y’|_x=a.

Функцияның туындысын табуды функцияны дифференциалдау деп те айтады.

Егер y=f(x) функциясының x=x₀ нүктесінде туындысы бар болса, яғни төмендегі шек бар болса:

онда біз y=f(x) функциясы x=x₀ нүктесінде дифференциалданады деп те айтамыз.

Теорема. Егер y=f(x) функциясы x=x₀ нүктесінде дифференциалданатын функция болатын болса (туындысы бар функция болатын болса) онда ол функция осы нүктеде үзіліссіз функция болады.