Анықталған интегралдардың қасиеттері
Теорема 1 (қосындының интегралы). Сандары шектеулі болатын функциялардың қосындысының анықталған интегралы сол функциялардың анықталған интегралдарының қосындысына тең болады:
мұнда u,v,…,w функциялар, x тәуелсіз айнымалы. Теорема 2 (тұрақты көбейткішті интегралдың алдына шығару). Интеграл астындағы функция көбейтіліп тұрған тұрақты санды интеграл белгісінің алдына шығаруға болады:
мұнда u функция, x оның аргументі, с тұрақты сан. Теорема 3 (интегралдау шектерінің орындарын ауыстыру). Егер анықталған интегралдың жоғарғы жіне төменгі шектерінің орындарын ауыстырса, онда анықталған интегралдың таңбасы қарама-қарсы таңбаға өзгереді:
Егер a=b болса
Теорема 4 (интегралдау интервалын бөлу). Егер [a,b] интегралдау интервалын [a,c], [c,b] екі бөліккее бөлсек, онда
Интегралды бағалау. Орта мән туралы теорема
Бұл тақырыпта анықталған интегралды бағалау сөз болады.
мұнда m және M сандары f(x) функциясының [a,b] аралығындағы төменгі және жоғарғы мәндері. Теорема 2. Егер [a,b] интервалының әрбір нүктесінде ψ(x)≤f(x)≤ϕ(x) болатын болса, онда
Теорема 3 (орта мән туралы). Анықталған интеграл есептеліп отырған [a,b] аралығында ең болмағанда бір x=ξ; нүктесі табылып
теңдігі орындалады.
|
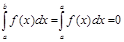
Теорема 1 (анықталған интегралды бағалау). Анықталған интегралдың мәні функцияның төменгі және жоғарғы мәндерін интегралдау аралығының ұзындығына көбейткенде шыққан сандардың арасында жатады
