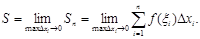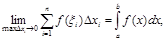Анықталған интеграл. Анықталған интегралдың бар болуы шарты. Анықталған интегралдың қасиеттері
a=x0≤ξ1≤x1≤ξ2≤x2≤…≤xn-1≤ξn≤xn=b. Енді табандары [xi-1,xi], i=1,2,…,n болатын, ал биіктіктері f(ξi) болатын тік төртбұрыштар салалық. Осы төртбұрыштардың аудандарын Si деп белгілелік. Сонда Sn осылардың қосындысы болсын. Енді осы кіші төртбұрыштардың табандарының ұзындығы ең үлкені нольге ұмтылсын, сонда кішілерінің бәрі де нольге ұмтылады. Сонда кіші төртбұрыштар аудандарының қосындысы қисық сызықты трапецияның ауданына ұмтылады, және бөліну нүктелерінің сандары шексіздікке ұмтылады. Сонымен:
Соңғы формуланың оң жағындағы өрнек интегралдық қосынды деп аталынады. Егер ол шек бар болса, ол шекті анықталған интеграл деп төмендегідей қылып белгілейді:
мұнда a интегралдың төменгі шегі, b интегралдың жоғарғы шегі деп аталынады. Анықталған интегралдың бар болуы туралы теорема. Егер y=f(x) функциясы [a,b] жабық аралығында үзіліссіз болса, онда оның n - ші интегралдық қосындысы бөліктеуден шыққан интервалдардың ең ұзынының ұзындығы нольге ұмтылғанда шегі бар. Ол шек, яғни анықталған интеграл
интеграл есептеліп отырған аралықты кіші интервалдарға қандай әдіспен бөлінгеннен тәуелсіз, кіші интервалдардың ішінен ξ1, ξ2, …, ξn нүктелерін таңдап алу әдісінен де тәуелсіз болады.
|

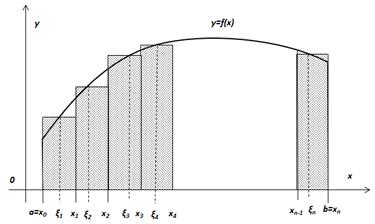 0xy координаталар системасында y=f(x) қисығы берілсін. y=f(x) функциясы [a,b] аралығында анықталған болсын. x=a, y=b түзулері, 0x осі және y=f(x) қисықтарынан құралған фигураны қисық сызықты трапеция деп атайды. Енді осы қисық сызықты трапецияның ауданын есептелік. Ол ауданды S әрпімен белгілелік. Осы ауданды есептеу үшін трапецияның табанын n бөліктерге бөлеміз.Бөліну нүктелерінен абсцисса осіне перпендикулярлар тұрғызып қисық сызықты трапецияны кіші қисық сызықты трапецияларға бөлеміз. Осы кіші қисық сызықты трапециялардың табандарын құрап түрған интервалдардыі әрқайсысынан біреуден ξ1, ξ2, …, ξn нүктелерін аламыз:
0xy координаталар системасында y=f(x) қисығы берілсін. y=f(x) функциясы [a,b] аралығында анықталған болсын. x=a, y=b түзулері, 0x осі және y=f(x) қисықтарынан құралған фигураны қисық сызықты трапеция деп атайды. Енді осы қисық сызықты трапецияның ауданын есептелік. Ол ауданды S әрпімен белгілелік. Осы ауданды есептеу үшін трапецияның табанын n бөліктерге бөлеміз.Бөліну нүктелерінен абсцисса осіне перпендикулярлар тұрғызып қисық сызықты трапецияны кіші қисық сызықты трапецияларға бөлеміз. Осы кіші қисық сызықты трапециялардың табандарын құрап түрған интервалдардыі әрқайсысынан біреуден ξ1, ξ2, …, ξn нүктелерін аламыз: