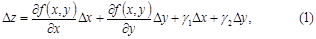Көп айнымалының функциясының дербес туындылары
Анықтама. z=f(x,y) функциясының x бойынша дербес туындысы деп функцияның Δxz дербес өсімшесінің Δx өсімшесіне қатынасының Δx ұмтылғанда шегі бар болса сол шекті айтамыз. z=f(x,y) функциясының x бойынша дербес туындысын төмендегі символдардың бірімен белгілейді.
Сонымен анықтама бойынша
Тап осылай етіп z=f(x,y) функциясының y айнымалысы бойынша дербес туындысын анықтауға болады. Ол дербес туынды да алдындағы сияқты төмендегі символдардың бірімен белгіленеді.
Сонымен
Δxz өсімшесін есептегенде y айнымалысын тұрақты қылып аламыз, ал Δyz өсімшесін есептегенде x айнымалысы тұрақты болады. Сондықтан дербес туындыларды басқаша былай анықтауға да болады: z=f(x,y) функциясының x айнымалысы бойынша дербес туындысы деп ол функцияның y айнымалысы тұрақты болған кезіндегі x бойынша туындысын айтамыз. Сол сияқты y айнымалысы бойынша дербес туындысы x айнымалысы тұрақты болған кездегі y айнымалысы бойынша туындысы болады екен. Соңғы анықтамадан дербес туындыны есептеген кезде кәдімгі туындыны есептеуде қолданған әдістерді қолдануға болатынын көреміз, тек қана туындыны есептеп отырған айнымалыдан басқа айнымалыға тұрақты сан есебінде қараймыз. Егер z=f(x,y) функциясының x, y аргументтері бойынша дербес туындылары бар болса, онда оның толық өсімшесін төмендегідей қылып жазуға болады екен:
мұнда γ1 және γ2 шамалары Δx пен Δy нольге ұмтылғанда нольге ұмтылатын, яғни
нольге ұмтылғанда нольге ұмтылатын шамалар. Сондықтан (1) формулада олардың әрқайсысы Δx, Δy өсімшелеріне көбейтіліп тұрғандықтан олардың ақырсыз аздық реті Δρ; шамасының ақырсыз аздық ретінен жоғары. (1) өрнектің алғашқы екі мүшесі Δx пен Δy өсімшелерінің бірінші дәрежесіне көбейтіліп тұр, егер f’x(x,y)≠0 және f’y(x,y)≠0 болса, онда бұл екі қосылғыш Δz функция өсімшесінің бас мүшесі болады. Бұл бас мүше Δz өсімшесінен тек Δρ; шамасына қарағанда жоғары ретті ақырсыз аз шамаға ғана ауытқиды. Анықтама. Егер z=f(x,y) функциясының Δz толық өсімшесі біріншісі Δx, Δy өсімшелерінен сызықты тәуелді болатын, ал екіншісі Δρ; шамасына қарағанда жоғары ретті ақырсыз аз шама болатын қосылғыштарға жіктелетін болса, бұл функция берілген нүктеде дифференциалданады деп айтады, ал функция өсімшесінің бірінші қосылғышы функцияның толық дифференциалы деп аталынады да dz, df символдарының бірімен белгіленеді. (1) теңдіктен егер f(x,y) функциясының берілген нүктеде үзіліссіз дербес туындылары бар болса, онда осы нүктеде функция дифференциалданады, оның толық дифференциалы төмендегі теңдікті қанағаттандырады:
Сондықтан (1), (2) өрнектерінен Δz≈dz екенін аламыз. Тәуелсіз айнымалылардың Δx, Δy өсімшелерін x, y тәуелсіз айнымалылардың дифференциалдары деп атап сәйкес dx, dy деп белгілейміз. Сонда толық дифференциалдың өрнегін мына түрде жазуға болады:
|