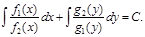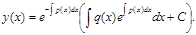Элементарлық әдістермен интегралданатын жай дифференциалдық теңдеудің кей түрлері

 

Кей жағдайда дифференциалдық теңдеуді мына түрде жазған қолайлы болады:

M(x,y)dx+N)x,y)dy=0.

Егер M(x,y), N(x,y) функцияларын тек қана x немесе y айнымалылардан ғана тәуелді болатын көбейткіштерге жіктей алсақ, дифференциалдық теңдеуді мына түрде жазуға болады:

f₁(x)g₁(y)dx+f₂(x)g₂(y)dy=0. (1)

g₁(y)≠0, f₂(x)≠0 деп есептеп дифференциалдық теңдеуді олардың көбейтіндісіне бөлсек теңдеу түрі төмендегідей болады:

Бұл дифференциалдық теңдеуді интегралдап оның жалпы интегралын мына түрде жазуға болады:

Берілген (1) дифференциалдық теңдеуді айнымалылары ажыратылатын теңдеу деп атайды.

Егерде кез-келген t үшін f(tx,ty)=t^αf(x,y) теңдігі орындалса, онда f(x,y) функциясы х және у аргументтері бойынша α (α=const) өлшемді біртектес функция деп аталады. Егер α=0 болса, онда біртектестік өлшемі ноль болады.

Егер M(x,y) және N(x,y) функциялары х және у аргументтері бойынша өлшемдері бірдей біртектес функциялар болса, яғни M(tx.ty)=t^αM(x,y), N(tx,ty)=t^αN(x,y) болса, онда

M(x,y)dx+N)x,y)dy=0

дифференциалдық теңдеуі біртектес дифференциалдық теңдеу деп аталынады.

Дифференциалдық теңдеуді мына түрге келтірелік:

Онда f(x,y) функциясы өлшемі ноль болатын біртектес функция боладың шынында

Бірінші ретті дифференциалдық теңдеу біртектес болған кезде оны түрінде жазуға болатындықтан, белгілеуін енгізіп теңдеуді мына түрге келтіруге болады:

Бұл теңдеуде z=y/x, y=zx, y’=z’x+z белгілеуін қолдансақ айнымалылары ажыратылған теңдеуге келеді:

Айнымалыларды ажыратып, шыққан теңдеуді интегралдап, бұрынғы белгілеулерге қайта оралу арқылы әуелгі біртектес теңдеудің жалпы интегралын табамыз.

Егер дифференциалдық теңдеу y’+p(x)y=q(x) түрінде болса, онда оны сызықтық дифференциалдық теңдеу деп атайды. Егер q(x)=0 болса, сызықтық дифференциалдық теңдеуді біртектес сызықтық дифференциалдық теңдеу деп атайды, олай болмаған жағдайда теңдеу біртектес емес сызықтық теңдеу деп аталады. Бірінші ретті сызықтық дифференциалдық теңдеуді y=uv (u және v белгісіз функциялар) белгілеулерін енгізу арқылы шешіп жалпы шешімін мына түрде алады: