Дифференциалдық теңдеулер. Бірінші ретті дифференциалдық теңдеулер
Анықтама. Тәуелсіз x айнымалысын, белгісіз y=f(x) функциясын және оның y’, y”, …, y(n) туындыларын байланыстыратын теңдеуді дифференциалдық теңдеу деп айтады. Символды түрде дифференциалдық теңдеуді былай
немесе былай
жазады. Егер белгісіз функциясы тек бір ғана аргументтен тәуелді болса дифференциалдық теңдеуді жай дифференциалдық теңдеу деп атайды. Біз тек қана жай дифференциалдық теңдеуді қарастырамыз. Анықтама. Теңдеудегі белгісіз функцияның туындыларының ең жоғарғы ретін дифференциалдық теңдеудің реті дейді. Анықтама. Егер y=ϕ(x) функциясын теңдеуге апарып қойғанда ол теңдеуді қанағаттандырса, яғни теңдеуді тепе-теңдікке айналдырса, бұл функцияны дифференциалдық теңдеудің шешімі немесе интегралы деп айтады. Бірінші ретті жай дифференциалдық теңдеудің жалпы түрі мынадай болады: F(x,y,y’)=0. Кейде бұл теңдеуді белгісіз функцияның туындысы арқылы шешуге болады: y’=f(x,y) (1) Бұл жағдайда біз дифференциалдық теңдеу туындысы арқылы шешіліп тұр деп айтамыз. Осындай теңдеулер үшін шешімі бар және жалғыз болуы туралы теореманы келтірелік. Теорема. Егер (1) теңдеудің оң жағындағы f(x,y) функциясы және оның y бойынша дербес f’y туындысы (x0,y0) нүктесін қамтитын 0xy жазықтығының D обылысында үзіліссіз болса, онда (1) дифференциалдық теңдеудің x=x0 y=y0 шартын қанағаттандыратын жалғыз шешімі болады. Егер геометриялық тұрғыдан қарайтын болсақ, графигі (x0,y0) нүктесі арқылы өтетін (1) теңдеуді қанағаттандыратын жалғыз ғана функция болады. Теоремадан (1) теңдеудің әртүрлі шексіз көп шешімі болатыны шығады. Мысалы теорема бойынша графиктері D обылысында жататын (x0,y1); (x0,y2);... нүктелері арқылы өтетін шешімдер болады, олар әртүрлі болады. Дифференциалдық теңдеу шешімі x=x0 болғанда y=y0 болуы керек деген шартты бастапқы шарт деп айтады. Бұл шартты кейде былай жазады
Анықтама. Егер бір кез-келген тұрақты санынан тәуелді болатын y=ϕ(x,C), (2) функциясы төмендегі шарттарды қанағаттандырса, бұл функцияны дифференциалдық теңдеудің жалпы шешімі деп айтады. 1. функциясы C санының кез-келген мәнінде дифференциалдық теңдеудің шешімі болады, яғни теңдеуді қанағаттандырады; 2. дифференциалдық теңдеудің шешімі бар және жалғыз болуы туралы теореманың шартын қанағаттандыратын кез-келген Теңдеудің шешімін іздеген кезде кей жағдайда шешім қанағаттандыратын мынандай теңдеу аламыз Φ(x,y,C)=0 (3) Бұл теңдеу дифференциалдық теңдеудің шешімін айқын емес түрде анықтап тұр. Мұндай жағдайда біз (3) өрнекті дифференциалдық теңдеудің жалпы интегралы деп айтамыз. Анықтама. Жалпы шешімдегі тұрақты сан бір мән қабылдаған кезде шыққан шешімді дифференциалдық теңдеудің дербес шешімі деп айтамыз, яғни C=C0 болса, онда y=ϕ(x,C0) дербес шешім болады. Дифференциалдық теңдеуді шешуді кейде дифференциалдық теңдеуді интегралдау деп те айтады. Сонымен дифференциалдық теңдеуді интегралдау дегеніміз: 1. егер бастапқы шарт берілмесе теңдеудің иә жалпы шешімін, иә жалпы интегралын табу; 2. егер бастапқы шарт берілсе, осы бастапқы шартты қанағаттандыратын дербес шешімін табу. Дифференциалдық теңдеудің берілген бастапқы шартты қанағаттандыратын шешімін табу есебін Коши есебі деп атайды. Дифференциалдық теңдеудің дербес шешімі жазықтықтағы декарттық координаталар системасында бір қисықтың теңдеуі болады. Бұл қисықты интегралдық қисық; деп атайлы. Дифференциалдық теңдеудің жалпы шешімі дифференциалдық теңдеудің барлық интегралдық қисықтарының жиынын береді.
|




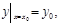 бастапқы шарт үшін C=C0 мәні табылып y=ϕ(x,C0) функциясы осы бастапқы шартты қанағаттандырады.
бастапқы шарт үшін C=C0 мәні табылып y=ϕ(x,C0) функциясы осы бастапқы шартты қанағаттандырады.


