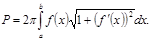Анықталған интегралды қолдану мысалдары
Анықталған интегралдың анықтамасынг берген кезде біз оның қисық сызықты трапецияның ауданын есептеуде қолданатынын көрген болатынбыз. Яғни y=f(x) қисық сызықты трапецияны анықтап тұрған қисықтың теңдеуі болатын болса, онда осы трапецияның ауданы S (y≥0 деп есептелік) функциясынан a -дан b -ға дейін (a мен b сандары (a<b) қисық сызықтың басы мен соңының абсциссалары) есептелген анықталған интегралына тең болады:
Енді қисық сызықты трапецияны анықтап тұрған қисық өзінің параметрлік теңдеуімен берілсін x=ϕ(t), y=ψ(t), онда x=ϕ(t) формуласы бойынша анықталған интегралда интеграл айнымалысына алмастыру енгізсек мынандай анықталған интеграл аламыз:
мұнда t айнымалысы t1 және t2 сандарының арасында өзгерген кезінде қисықтың барлық нүктелерін аламыз. Мысал. Мына эллипс
шектеп тұрған фигураның ауданын табыңыз. Шешімі. Эллипстің жоғарғы жартысының ауданын есептеп 2 санына көбейтеміз. Сонымен:
Бұл ауданды есептегенде эллипстің параметрлік теңдеуін қолдану қолайлвһырақ болады: x=acost, y=bsint. Сонда
Қисықтың доғасының ұзындығын есептеу. y=f(x) теңдеуімен берілген қисықта жатқан A, B нүктелерін алалық. Онда AB доғасының ұзындығы осы нүктелерді қосып тұрған, төбелері берілген қисықтың A мен B нүктелерінің аралығында орналасқан сынық сызықтың ұзындығының осы сынық сызықтың ең ұзын қабырғасының ұзындығы нольге ұмтылғандағы шегіне тең болады. Егер бұл шек бар болса оны мына формуламен есептеуге болады:
Егер қарастырып отырған қисық x=x(t), y=y(t) параметрлік теңдеулерімен берілсе (t параметрінің қисық доғасының шеттеріне сәйкес келетін параметр мәндері t1,t2 (t1<t2) болсын) доға ұзындығы былай есептеледі:
Енді қисық полярлық координаталар системасындағы теңдеуімен берілсін r=r(ϕ). Полярлық және декарттық координаталар системасының арасында x=rcosϕ, y=rsinϕ; байланысы барын ескеріп ϕ полярлық бұрышты параметр есебінде қарастырсақ мынаны аламыз: dx=(r’cosϕ-rsinϕ)dϕ, dy=(r’sinϕ+rcosϕ)dϕ. Бұдан
аламыз. Сондықтан
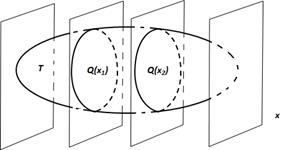
Параллель қималардың аудандарының көмегі арқылы дененің көлемін есептеу. Бізге T денесі берілсін. 0x осіне перпендикуляр жазықтықтармен қиғандағы қималардың аудандары Q(x) белгілі болсын. Онда бұл аудандарды x -тен тәуелді Q=Q(x) функциясы ретінде қарастыруға болады. x –қиюшы жазықтықтың абсцисса осін қиып өткен нүктесінің абсциссасы. функциясы үзіліссіз функция болсын. Дене абсцисса осін x=a, x=b нүктелерінде қиып өтетін, абсцисса осіне перпендикуляр жазықтықтардың арасында орналассын. Онда қарастырыпи отырған көлем мына формуламен есептеледі:
формуласымен есептеледі. Ал осы айналудан шыққан беттің ауданы мына формуламен есептеледі:
|


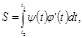
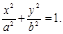
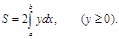
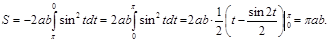
 Енді фигураны шектеп тұрған сызық полярлық координаталар системасындағы теңдеуімен берілген жағдайды қаралық. Бұл жағдайда қисық сызықты трапецияның орнына қисық сызықты сектордың ауданын есептейміз. Сектор теңдеуі r=f(ϕ) болатын қисықпен және полюстен басталатын ϕ=α, ϕ=β сәулелерімен шектелген фигура болсын. Онда бұл қисық сызықты сектордың ауданы мынаған тең болады:
Енді фигураны шектеп тұрған сызық полярлық координаталар системасындағы теңдеуімен берілген жағдайды қаралық. Бұл жағдайда қисық сызықты трапецияның орнына қисық сызықты сектордың ауданын есептейміз. Сектор теңдеуі r=f(ϕ) болатын қисықпен және полюстен басталатын ϕ=α, ϕ=β сәулелерімен шектелген фигура болсын. Онда бұл қисық сызықты сектордың ауданы мынаған тең болады: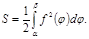

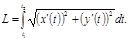

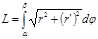
 мұнда α; мен β; сандары полярлық бұрыштың доғаның А мен В шеттетіне сәйкес келетін мәндері.
мұнда α; мен β; сандары полярлық бұрыштың доғаның А мен В шеттетіне сәйкес келетін мәндері.
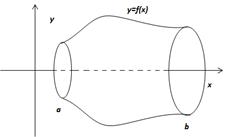 Айналу денесінің көлемі мен оның бетінің ауданы. Кеңістікте декарттық координаталар системасын қарастыралық. 0xy жазықтығында теңдеуі y=f(x) болатын x=a, x=b түзулерімен шектелген қисық сызықты трапецияны қарастыралық. Осы трапецияны 0x осін айналдыра толық шеңбер жасата бұрсақ айналу денесін аламыз. Бұл дененің 0x осіне перпендикуляр қималарының бәрі де центрі 0x осінде жататын дөңгелектер болады. Бұл дененің көлемі
Айналу денесінің көлемі мен оның бетінің ауданы. Кеңістікте декарттық координаталар системасын қарастыралық. 0xy жазықтығында теңдеуі y=f(x) болатын x=a, x=b түзулерімен шектелген қисық сызықты трапецияны қарастыралық. Осы трапецияны 0x осін айналдыра толық шеңбер жасата бұрсақ айналу денесін аламыз. Бұл дененің 0x осіне перпендикуляр қималарының бәрі де центрі 0x осінде жататын дөңгелектер болады. Бұл дененің көлемі