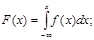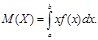Зіліссіз кездейсоқ шаманың таралу функциясы мен тығыздығы

 

Үзіліссіз кездейсоқ шаманың таралу заңын дискретті кездейсоқ шамадағыдай қылып таблица арқылы беру мүмкін емес. Үзіліссіз кездейсоқ шаманы бергенде таралу функциясын немесе таралу тығыздығы арқылы береді.

Үзіліссіз кездейсоқ X шамасының сынақ кезінде қабылдайтын мәні x тан кіші болуының ықтималдылығын F(x) деп белгілеп осы үзіліссіз кездейсоқ шаманың таралу функциясы деп атайды. Яғни таралу функциясы мына теңсіздік көмегі арқылы анықталады

F(x)=P(X<x).

Кейде таралу функциясын интегралдық функция деп атайды.

Таралу функциясының қасиеттері:

1. 0≤F(x)≤1;

2. x₂>x₁→F(x₂)≥F(x₁);

3. P(a≤X<b)=P(a≤X≤b)=P(a<X≤b)=P(a<X<b)=F(b)-F(a);

4. Егер үзіліссіз кездейсоқ шаманың мүмкін мәндері (a,b) аралығында жатса, онда 1) f(x)=0 егер x≤a болса; 2) F(x)=1 егер x≥b болса.

Таралу функциясының графигі қ саны мен 1 саны шектеп тұрған жолаққа орналасады. Таралу функциясы кемімейтін функция болғандықтан оның графигі оңға жылжығанда төмен түспейді, тек жоғарыға қарай көтерілуі мүмкін, бірақ 1 санынан асып кетпейді.

Үзіліссіз кездейсоқ шаманың таралу функциясының бірінші ретті туындысын ықтималдылықтардың таралу тығыздығы деп атайды.

Сонымен егер F(x) үзіліссіз кездейсоқ X шамасының таралу функциясы болса, ал f(x) таралу тығыздығы болатын болса, онда

f(x)=F’(x).

болады.

Ықтималдылықтардың таралу тығыздығын кейде үзіліссіз кездейсоқ шаманың дифференциалдық функциясы деп айтады. Таралу функциясын дискретті кездейсоқ шама үшін де беруге болады, ал таралу тығыздығы тек үзіліссіз кездейсоқ шама үшін анықталады.

Ықтималдылықтардың таралу тығыздығының қасиеттері:

1.

2.

3.

4.

Кездейсоқ X шамасының мүмкін мәндері (a,b) аралығында жатсын (бұл аралық -∞; пен ∞; тің аралығы болуы да мүмкін). Онда осы кездейсоқ шаманың математикалық күтімі деп төменгі формуламен анықталатын санды айтады

(a,b) аралығында мүмкін мәндері жататын үзіліссіз X кездейсоқ шамасының дисперсиясы деп оның математикалық күтімнен ауытқуының квадратының математикалық күтімін айтады. Яғни дисперсия мына формуламен анықталады

Төмендегі формуламен анықталатын шаманы орта квадраттық ауытқу деп атайды