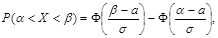Нормаль таралу заңы
Үзіліссіз кездейсоқ шаманың ықтималдылығының таралу тығыздығы мына формуламен
анықталатын болса, онда ол нормаль таралу заңымен таралып тұр деп айтамыз. Нормаль таралу заңымен таралған үзіліссіз кездейсоқ шама үшін M(x)=a, D(X)=σ2 теңдіктері орындалады. Нормаль таралу заңының тығыздығының графигін нормаль қисық; деп атайды. Кейде нормаль қисықты Гаусс қисығы деп те атайды. Егер X үзіліссіз кездейсоқ шамасы нормаль заңымен таралған болса, оның мүмкін мәндері [α,β] аралығында жатуының ықтималдыдығы
формуласымен есептеледі. Мұнда Лаплас функциясы. Нормаль таралған үзіліссіз кездейсоқ шаманың мүмкін мәндерінің оның математикалық күтімінен ауытқуы δ; шамасынан аспауының ықтималдылығы былай есептеледі
Егер δ=3σ; болса, онда
яғни кездейсоқ шаманың математикалық күтімнен ауытқуы үш еселенген орта квадраттан аспауының ықтималдылығы 0,9973 болады екен. Мұны үш сигма ережесі деп атайды. Іс жүзінде нормаль таралған үзіліссіз кездейсоқ шамалар өте жиі кездеседі. Мұны немен түсіндіруге болады? Бұған А.М.Ляпуновтың орталық теоремасы жауап бере алады. Егер X кездейсоқ шамасы өте көп тәуелсіз кездейсоқ шамалардың қосындысынан құралса, олардың әрқайсысының X кездейсоқ шамасына әсері тым аз болатын болса, онда X кездейсоқ шамасының таралу заңы нормаль таралу заңына өте жақын болады.
Математикалық статистика элементтері
|