Решение. Очевидно, при всех допустимых значениях и .
Очевидно, Равенство достигается, когда оба слагаемых одновременно равны нулю, т.е. когда
Ответ: 0; при
2.3. Решите уравнение Решение.
Ответ: -3; 2.6. Решите уравнение Решение. Пусть Вернемся к старой переменной. 1) 2) Ответ:
2.8. Решите уравнение Решение.
1 способ.
Ответ: -3; 2 способ. О.О.У.
На области определения имеем
Ответ: -3; 3 способ.
Проверка: 1) 2) Ответ: -3;
2.21. Вычислите координаты точек пересечения парабол Решение. Абсциссы точек пересечения парабол являются корнями уравнения Если Если Значит, параболы имеют две точки пересечения, координаты которых Ответ:
2.22. Решите уравнение Решение. 1) Так как 1-25+60-36=0, то 1 – корень исходного уравнения.
2) Так как
3) Ответ:-6; 1; 2; 3. 2.30. Найдите все целые значения Решение. При При Решим систему Это множество содержит четыре целых числа: -2; -1; 1; 2. Ответ: -2; -1; 1; 2.
2.31. При каком значении Решение. Исходное уравнение может иметь два корня в двух случаях. 1) Уравнение 2) Один из корней уравнения Ответ: 0 и -3 при 0 и -6 при
2.32. При каких значениях Решение. 1 способ.
Ответ: при всех 2 способ.
Это уравнение имеет корни при Ответ: при всех
2.41. Решите систему уравнений Решение. Данная система является симметричной системой четвертой степени, значит, она имеет не более четырех решений. Очевидно, решениями являются следующие пары чисел Ответ:
2.50. Решите систему уравнений Решение. Система из двух первых уравнений имеет единственное решение, т.к. коэффициенты при неизвестных непропорциональны. Если это решение удовлетворяет третьему уравнению, то оно и есть решение исходной системы. Если это решение не удовлетворяет третьему уравнению, то система решений не имеет. 1) 2) Ответ: решений нет.
2.59. При каких значениях Решение. Рассмотрим функцию
. Ответ:
2.60. При каких значениях Решение. Данное квадратное уравнение имеет два различных корня
Ответ: при всех
2.62. Докажите, что уравнение Доказательство.Преобразуем левую часть данного уравнения. Равенство достигается только, если имеет решения система. Так как эта система решений не имеет, то выражение в левой части уравнения при любых значениях больше 1. Следовательно, исходное уравнение корней не имеет, ч.т.д.
2.63. Докажите, что число 1 является корнем уравнения Доказательство.1 способ.. Обозначим, тогда и уравнение примет вид;; или. Значит, или. Первое уравнение имеет единственный корень, равный 1. Второе уравнение корней не имеет. Следовательно, исходное уравнение имеет единственный корень, который равен 1, ч.т.д. 2 способ. При Пусть
2.71. Решите систему уравнений Решение.
1) 2) Ответ:
2.74. При каких значениях Решение.
Ответ: при
2.77. Решите систему уравнений Решение. 1 способ. Ответ: 2 способ. Сложив все четыре уравнения системы, получим уравнение Ответ:
|

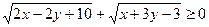 при всех допустимых значениях
при всех допустимых значениях  и
и  .
. ;
; 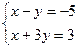 ;
; 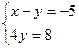 ;
;  ;
;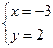 .
.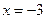 ,
, 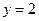 .
.
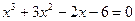 .
.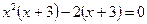 ;
;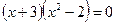 ;
;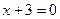 или
или 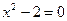 ;
; или
или  ;
; или
или 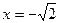 .
.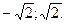
 .
.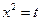 , тогда
, тогда 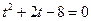 ;
;  или
или 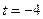 .
.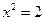 ;
; 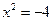 - корней нет.
- корней нет.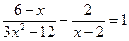 .
.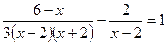
 .
. ;
; 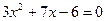 ;
;  ;
; или
или 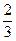 .
.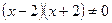
 и
и 
 .
.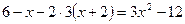 ;
;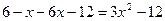 ;
;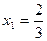 или
или  . Оба значения входят в область определения уравнения.
. Оба значения входят в область определения уравнения.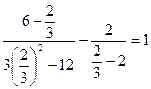 ;
; 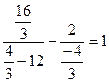 ;
;  ;
; 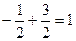 - верно, значит
- верно, значит 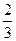 - корень уравнения.
- корень уравнения.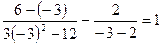 ;
;  ;
;  -верно, значит -3- корень уравнения.
-верно, значит -3- корень уравнения.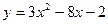 и
и 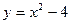 .
.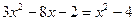 ;
; 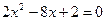 ;
; 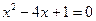 ;
; 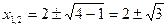 .
.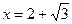 , то
, то  .
.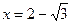 , то
, то 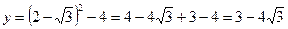 .
.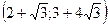 и
и  .
.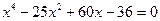 .
.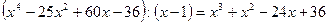 .
. .
. - верно, то 2 – корень этого уравнения.
- верно, то 2 – корень этого уравнения. .
. ;
;  или
или  .
.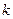 , при которых уравнение
, при которых уравнение 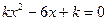 имеет два корня.
имеет два корня.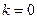 имеем
имеем 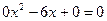 ;
; 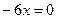 - это уравнение имеет один корень.
- это уравнение имеет один корень. исходное уравнение квадратное. Оно имеет два корня тогда и только тогда, когда
исходное уравнение квадратное. Оно имеет два корня тогда и только тогда, когда 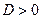 .
. 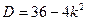 .
.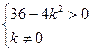 ;
; 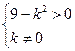 ;
;  ;
; 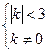 ;
;  ;
;  .
. уравнение
уравнение  имеет два корня? Найдите эти корни.
имеет два корня? Найдите эти корни.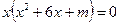 ;
;  или
или 
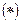 .
.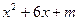 - полный квадрат, значит,
- полный квадрат, значит,  .
.  . Тогда
. Тогда  .
.  ;
; 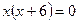 ;
;  уравнение
уравнение  имеет корни?
имеет корни? . Это квадратное уравнение имеет корни, если
. Это квадратное уравнение имеет корни, если 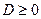 .
.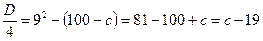 .
. , т.е.
, т.е. 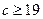 .
.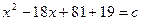 ;
;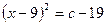 .
. , т. е. при
, т. е. при 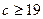 .
.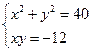 .
. ;
; 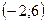 ;
; 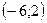 ;
; 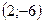 .
. .
. ;
;  ;
; 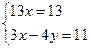 ;
; 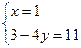 ;
;  .
.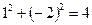 - неверно, значит, исходная система решений не имеет.
- неверно, значит, исходная система решений не имеет. один корень квадратного уравнения
один корень квадратного уравнения 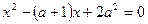 больше
больше  , а другой меньше
, а другой меньше 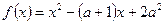 , графиком которой является парабола. Так как старший коэффициент положительный, то ветви параболы направлены вверх. По условию задачи корни лежат по разные стороны от числа
, графиком которой является парабола. Так как старший коэффициент положительный, то ветви параболы направлены вверх. По условию задачи корни лежат по разные стороны от числа  , т.е.
, т.е. 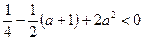 ;
; 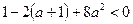 ;
; 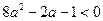 ;
; 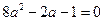 ;
; 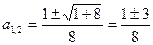 ;
;  или
или 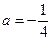 .
.
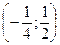 .
. уравнение
уравнение 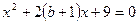 имеет два различных положительных корня?
имеет два различных положительных корня? и
и  , если
, если 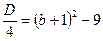 ). Поскольку
). Поскольку  , а
, а 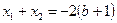 , то положительными корни будут, если
, то положительными корни будут, если  . Значит, условию задачи удовлетворяют все решения системы
. Значит, условию задачи удовлетворяют все решения системы 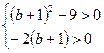 ;
; 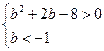 .
.
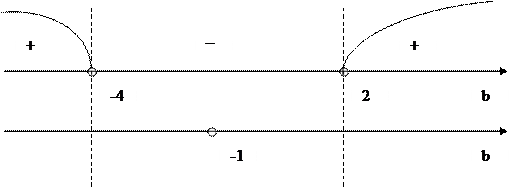
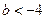 .
. не имеет корней.
не имеет корней.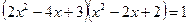 и других корней у этого уравнения нет.
и других корней у этого уравнения нет.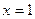 имеем
имеем  ;
; 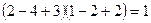 - верно, значит 1 – корень уравнения.
- верно, значит 1 – корень уравнения. , тогда
, тогда 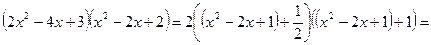
 , значит при
, значит при 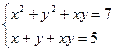 .
.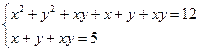 ;
; 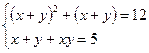 .
.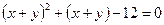 - квадратное уравнение относительно
- квадратное уравнение относительно  , решая его, получаем
, решая его, получаем  или
или 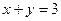 .
.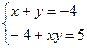 ;
;  ;
;  ;
; 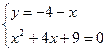 - решений нет.
- решений нет.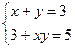 ;
;  - симметричная система второй степени, которая имеет не более двух решений. Очевидно, это пары чисел
- симметричная система второй степени, которая имеет не более двух решений. Очевидно, это пары чисел  и
и 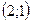 .
.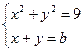 имеет единственное решение?
имеет единственное решение?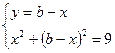 ;
; 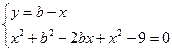 ;
; 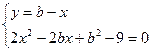 . Система имеет единственное решение, если у второго уравнения системы дискриминант равен нулю.
. Система имеет единственное решение, если у второго уравнения системы дискриминант равен нулю. 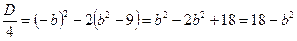 .
. ;
;  .
. или
или 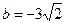 .
.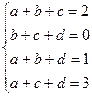 .
.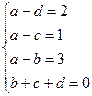 ;
; 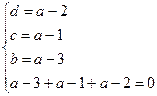 ;
; 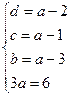 ;
;  ;
;  .
.
 , т.е.
, т.е.  . Вычитая почленно из него каждое из уравнений данной системы, последовательно получаем
. Вычитая почленно из него каждое из уравнений данной системы, последовательно получаем 


