5.4. Прямая 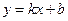 пересекает ось
пересекает ось 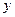 в точке
в точке  и проходит через точку
и проходит через точку  . Запишите уравнение этой прямой. В какой координатной четверти нет точек этой прямой?
. Запишите уравнение этой прямой. В какой координатной четверти нет точек этой прямой?
Решение. Первая часть задачи:
1 способ. Так как точки  и
и  лежат на прямой
лежат на прямой 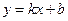 , то
, то
 ;
;  ;
;  ;
; 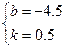 ,
,
значит уравнение искомой прямой имеет вид 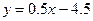 .
.
2 способ. Так как прямая 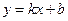 пересекает ось
пересекает ось 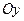 в точке
в точке  , то
, то  .
.
Так как точки  и
и  лежат на прямой
лежат на прямой 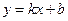 , то
, то 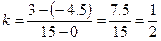 . Значит уравнение искомой прямой имеет вид
. Значит уравнение искомой прямой имеет вид 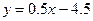 .
.
Вторая часть задачи:
Вообще говоря, если учащийся 9-го класса нарисовал график функции и на этом основании сделал вывод, что соответствующая прямая не содержит точек II четверти, то данная задача оценивается полным баллом. С другой стороны, ссылка на график без соответствующих пояснений всегда вызывает некоторые сомнения. Приведем одно из возможных решений, не содержащее подобных ссылок.
Прямая не содержит точек II четверти. Действительно. Предположим, что точка  , принадлежащая графику функции
, принадлежащая графику функции 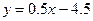 , лежит во II четверти, значит
, лежит во II четверти, значит 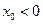 ,
, 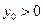 и
и  - верное числовое равенство. Тогда
- верное числовое равенство. Тогда  , т.е.
, т.е.  . Полученное противоречие показывает, что предположение не верно, т.е. данная прямая не содержит точек II четверти. Ч.т.д.
. Полученное противоречие показывает, что предположение не верно, т.е. данная прямая не содержит точек II четверти. Ч.т.д.
Ответ: 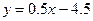 ; прямая не содержит точек II четверти.
; прямая не содержит точек II четверти.
5.14. Выясните, лежат ли на одной прямой точки 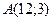 ,
,  и
и  .
.
Решение. 1 способ. Найдем уравнение прямой 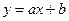 , проходящей через точки
, проходящей через точки 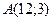 и
и  .
.
;;;.
Значит уравнение имеет вид  . Выясним, принадлежит ли этой прямой точка
. Выясним, принадлежит ли этой прямой точка 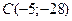 . Т.к.
. Т.к.  ,
,  - неверное числовое равенство, то точка
- неверное числовое равенство, то точка 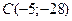 не лежит на прямой, проходящей через точки
не лежит на прямой, проходящей через точки 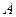 и
и 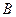 , т.е. эти три точки не лежат на одной прямой.
, т.е. эти три точки не лежат на одной прямой.
Ответ: точки 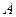 ,
, 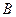 и
и  не лежат на одной прямой.
не лежат на одной прямой.
2 способ. Угловой коэффициент прямой, проходящей через точки 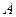 и
и 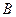 , равен
, равен 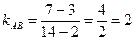 . Угловой коэффициент прямой, проходящей через точки
. Угловой коэффициент прямой, проходящей через точки 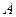 и
и  , равен
, равен 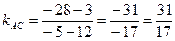 . Т.к.
. Т.к.  , то точки
, то точки 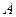 ,
, 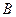 и
и  не лежат на одной прямой.
не лежат на одной прямой.
Ответ: точки 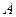 ,
, 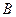 и
и  не лежат на одной прямой.
не лежат на одной прямой.
5.24. Прямая проходит через точку  и касается гиперболы
и касается гиперболы  . В какой точке эта прямая пересекает ось абсцисс?
. В какой точке эта прямая пересекает ось абсцисс?
Решение. 1 способ. Так как прямая проходит через точку  , то ее уравнение
, то ее уравнение  ; а т.к. она касается гиперболы
; а т.к. она касается гиперболы  , то уравнение
, то уравнение 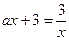 имеет единственное решение, причем
имеет единственное решение, причем  .
.
 ;
;  ;
;  ;
;  .
.
Значит эта прямая задается уравнением  . Абсцисса точки пересечения этой прямой удовлетворяет уравнению
. Абсцисса точки пересечения этой прямой удовлетворяет уравнению  ;
;  .
.
Ответ: 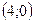 .
.

2 способ. Известно, что любая касательная, проведенная к гиперболе, отсекает от осей координат – треугольник постоянной площади.
Т.к. координаты вершины гиперболы  , то площадь треугольника равна
, то площадь треугольника равна  . Абсцисса искомой точки находится из уравнения
. Абсцисса искомой точки находится из уравнения  , т.е.
, т.е.  .
.
Ответ: 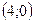 .
.
5.34. При каких значениях 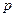 вершины парабол
вершины парабол  и
и  расположены по разные стороны от оси
расположены по разные стороны от оси 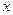 ?
?
Решение. 1 способ. Ордината вершины параболы  вычисляется по формуле
вычисляется по формуле 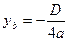 .
.
1. Если  , то
, то  .
.
2. Если  , то
, то 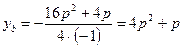 .
.
Вершины расположены по разные стороны от оси 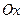 , если их ординаты имеют разные знаки, т.е.
, если их ординаты имеют разные знаки, т.е. 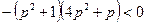 , т.е.
, т.е. 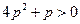 ;
; 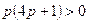 .
.
Ответ:  .
.
2 способ. Очевидно, при любом 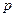 уравнение
уравнение  имеет два корня (разных знаков). Значит, вершина соответствующей параболы лежит в нижней полуплоскости. Вершина параболы
имеет два корня (разных знаков). Значит, вершина соответствующей параболы лежит в нижней полуплоскости. Вершина параболы  будет лежать в верхней полуплоскости тогда и только тогда, когда уравнение
будет лежать в верхней полуплоскости тогда и только тогда, когда уравнение 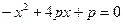 имеет два корня, т.е. если его дискриминант положителен.
имеет два корня, т.е. если его дискриминант положителен. 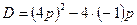 ;
;  ;
; 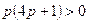 .
.
Ответ:  .
.
5.36. Найдите все значения 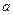 , при которых точка пересечения прямых
, при которых точка пересечения прямых  и
и  находится в первой координатной четверти?
находится в первой координатной четверти?
Решение. 1 способ. Координаты точки пересечения прямых являются решением системы 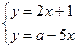 ;
; 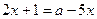 ;
;  ;
;  .
.
 ;
; 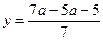 ;
;  .
.
Чтобы точка с координатами 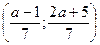 лежала в I четверти, должны выполняться условия:
лежала в I четверти, должны выполняться условия: 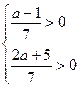 ;
; 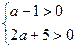 ;
; 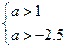 ;
;  .
.
Ответ:  .
.
2 способ. Изобразим схематически графики функций:  ;
;  ;
;  .
.
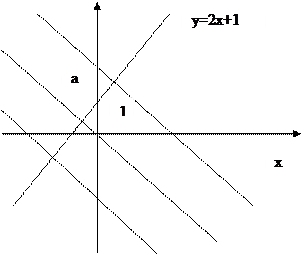
Из рисунка видно, что для того чтобы графики соответствующих функций пересекались в I четверти, должно выполняться неравенство  .
.
Ответ:  .
.
5.39. При каких значениях 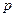 прямая
прямая 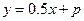 образует с осями координат треугольник, площадь которого равна
образует с осями координат треугольник, площадь которого равна  ?
?
Решение. Найдем координаты точек пересечения прямой 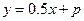 с осями координат.
с осями координат.
 :
:  ;
;  ;
; 
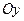 :
:  ;
;  ;
; 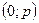
Значит  .
.
Тогда 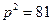 , т.е.
, т.е.  или
или  .
.
Ответ: при  или
или  .
.
5.40. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют уравнению  .
.
Решение. Так как  , то
, то  , т.е.
, т.е.  , откуда
, откуда 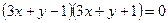 . Значит либо
. Значит либо  , либо
, либо  . Каждое из этих уравнений является уравнением прямой:
. Каждое из этих уравнений является уравнением прямой: 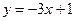 или
или 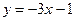 .
.




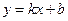 пересекает ось
пересекает ось 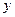 в точке
в точке  и проходит через точку
и проходит через точку  . Запишите уравнение этой прямой. В какой координатной четверти нет точек этой прямой?
. Запишите уравнение этой прямой. В какой координатной четверти нет точек этой прямой? ;
;  ;
;  ;
; 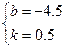 ,
,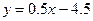 .
.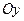 в точке
в точке  .
.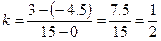 . Значит уравнение искомой прямой имеет вид
. Значит уравнение искомой прямой имеет вид  , принадлежащая графику функции
, принадлежащая графику функции 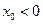 ,
, 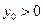 и
и  - верное числовое равенство. Тогда
- верное числовое равенство. Тогда  , т.е.
, т.е.  . Полученное противоречие показывает, что предположение не верно, т.е. данная прямая не содержит точек II четверти. Ч.т.д.
. Полученное противоречие показывает, что предположение не верно, т.е. данная прямая не содержит точек II четверти. Ч.т.д.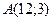 ,
,  и
и  .
.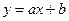 , проходящей через точки
, проходящей через точки  . Выясним, принадлежит ли этой прямой точка
. Выясним, принадлежит ли этой прямой точка 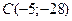 . Т.к.
. Т.к.  ,
,  - неверное числовое равенство, то точка
- неверное числовое равенство, то точка  и
и  , т.е. эти три точки не лежат на одной прямой.
, т.е. эти три точки не лежат на одной прямой. не лежат на одной прямой.
не лежат на одной прямой.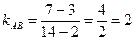 . Угловой коэффициент прямой, проходящей через точки
. Угловой коэффициент прямой, проходящей через точки 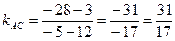 . Т.к.
. Т.к.  , то точки
, то точки  и касается гиперболы
и касается гиперболы  . В какой точке эта прямая пересекает ось абсцисс?
. В какой точке эта прямая пересекает ось абсцисс? ; а т.к. она касается гиперболы
; а т.к. она касается гиперболы 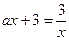 имеет единственное решение, причем
имеет единственное решение, причем  .
. ;
;  ;
;  ;
;  .
. . Абсцисса точки пересечения этой прямой удовлетворяет уравнению
. Абсцисса точки пересечения этой прямой удовлетворяет уравнению  ;
;  .
.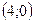 .
.
 , то площадь треугольника равна
, то площадь треугольника равна  . Абсцисса искомой точки находится из уравнения
. Абсцисса искомой точки находится из уравнения  , т.е.
, т.е. 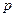 вершины парабол
вершины парабол  и
и  расположены по разные стороны от оси
расположены по разные стороны от оси 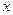 ?
? вычисляется по формуле
вычисляется по формуле 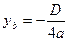 .
. .
.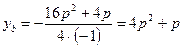 .
.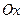 , если их ординаты имеют разные знаки, т.е.
, если их ординаты имеют разные знаки, т.е. 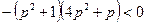 , т.е.
, т.е. 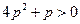 ;
; 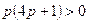 .
. .
. имеет два корня (разных знаков). Значит, вершина соответствующей параболы лежит в нижней полуплоскости. Вершина параболы
имеет два корня (разных знаков). Значит, вершина соответствующей параболы лежит в нижней полуплоскости. Вершина параболы  будет лежать в верхней полуплоскости тогда и только тогда, когда уравнение
будет лежать в верхней полуплоскости тогда и только тогда, когда уравнение 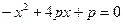 имеет два корня, т.е. если его дискриминант положителен.
имеет два корня, т.е. если его дискриминант положителен. 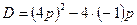 ;
;  ;
; 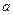 , при которых точка пересечения прямых
, при которых точка пересечения прямых  и
и  находится в первой координатной четверти?
находится в первой координатной четверти?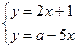 ;
; 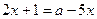 ;
;  ;
;  .
. ;
; 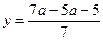 ;
;  .
.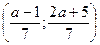 лежала в I четверти, должны выполняться условия:
лежала в I четверти, должны выполняться условия: 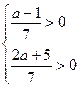 ;
; 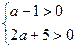 ;
; 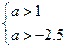 ;
;  .
. ;
;  .
.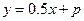 образует с осями координат треугольник, площадь которого равна
образует с осями координат треугольник, площадь которого равна  ?
? :
:  ;
;  ;
; 
 ;
;  ;
; 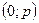
 .
.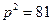 , т.е.
, т.е.  или
или  .
. .
. , т.е.
, т.е.  , откуда
, откуда 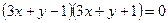 . Значит либо
. Значит либо  , либо
, либо  . Каждое из этих уравнений является уравнением прямой:
. Каждое из этих уравнений является уравнением прямой: 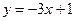 или
или 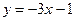 .
.


