Арифметическая и геометрическая прогрессии.
6.1. Пятый член арифметической прогрессии равен 8,4, а ее десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии. Решение. 1 способ. Из условия задачи следует, что Значит, Так как Ответ: 2 способ. Из свойств арифметической прогрессии следует, что Ответ:
6.3. Первый член арифметической прогрессии равен 6, а ее разность равна 4.Начиная с какого номера члены этой прогрессии больше 260? Решение. Так как Наименьшее натуральное n, удовлетворяющее этому неравенству, равно 65. Ответ:
6.6. Найдите сумму всех последовательных натуральных чисел с 60 до 110 включительно. Решение. Сумму 60+61+…+110 естественно рассматривать как сумму 51 члена арифметической прогрессии с Ответ:4335.
6.8. В геометрической прогрессии Решение. Из условия задачи следует, что Ответ:
6.14. Существует ли арифметическая прогрессия, в которой Решение. Предположим, что данная прогрессия существует. Так как Так как Т. е. Ответ: не существует.
6.22. Существует ли геометрическая прогрессия, в которой, Решение. 1 способ. Очевидно, геометрическая прогрессия с Так как Ответ: существует. 2 способ. Да, существует. Например, геометрическая прогрессия, у которой Ответ: существует.
6.28. Найдите сумму первых 20 совпадающих членов двух арифметических прогрессий: 3, 8, 13,… и 4, 11, 18,…. Решение. Совпадающие члены данных прогрессий также образуют арифметическую прогрессию. Выписав несколько первых членов этих прогрессий: 3; 8; 13; 18; 23;… и 4; 11; 18; 25;…, находим, что первый член новой прогрессии равен 18. Так как разность первой прогрессии равна 5, а второй – 7, а 5 и 7 – взаимно простые числа, то разность новой прогрессии равна 35. Итак, следует найти сумму 20 членов арифметической прогрессии, у которой Ответ: 7010.
6.29. Решите уравнение Решение. Выражение, стоящее в левой части уравнения, естественно рассматривать как сумму сорока членов арифметической прогрессии с Эта сумма равна Ответ: 1. 6.30. Решите уравнение Решение. Из условия задачи следует, что Ответ: 19.
6.33. Сколько существует натуральных трехзначных чисел, которые делятся только на одно из чисел 4 или 5? Решение. Из условия задачи следует, что искомые числа - это трехзначные числа, делящиеся либо на 4, либо на 5, но при этом не делящиеся на 20. Первые числа: 100; 104;…;996. Их количество Ответ: 315.
6.35. В арифметической прогрессии среднее арифметическое первых десяти ее членов равно 20. Найдите первый член и разность этой прогрессии, если известно, что они являются числами натуральными. Решение. Из условия задачи следует, что При При При
Ответ:
|

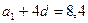 ;
; 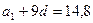 .
.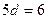 .
.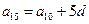 , то
, то 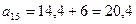 .
.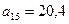 .
.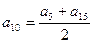 . Значит,
. Значит, 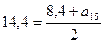 ;
; 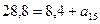 ;
; 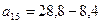 ;
; 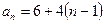 , то для решения задачи достаточно найти наименьшее натуральное n, при котором верно неравенство
, то для решения задачи достаточно найти наименьшее натуральное n, при котором верно неравенство 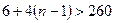 ;
;  ;
; 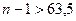 ;
; 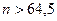 .
.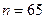 .
.
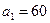 и
и 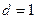 . Тогда
. Тогда 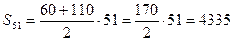 .
.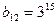 и
и 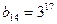 . Найдите
. Найдите 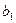 .
.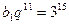 ;
; 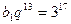 . Значит
. Значит 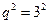 , т.е.
, т.е. 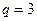 или
или 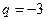 . Если
. Если  . Если
. Если 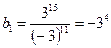 .
. или
или 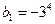 .
.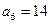 ,
, 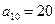 и
и 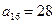 ?
?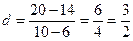 .
.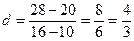 .
.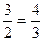 - противоречие, следовательно, предположение неверно. Требуемой прогрессии не существует.
- противоречие, следовательно, предположение неверно. Требуемой прогрессии не существует.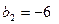 ,
, 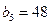 и
и 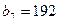 ?
?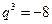 ,
, 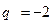 .
.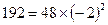 - верное числовое равенство, то 192 является седьмым членом этой прогрессии. Значит, геометрическая прогрессия, удовлетворяющая условию задачи, существует.
- верное числовое равенство, то 192 является седьмым членом этой прогрессии. Значит, геометрическая прогрессия, удовлетворяющая условию задачи, существует.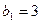 и
и 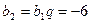 ;
; 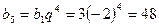 ;
; 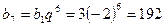 .
.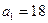 ;
; 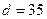 ;
; 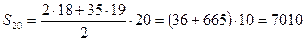 .
.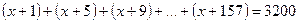 .
.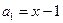 и
и 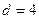
 .
.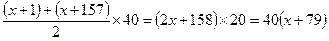 . Таким образом исходное уравнение принимает вид
. Таким образом исходное уравнение принимает вид 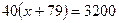 , откуда
, откуда 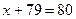 ;
; 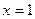 .
.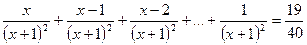 .
.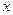 - натуральное число. Каждое слагаемое в левой части уравнения содержит общий множитель
- натуральное число. Каждое слагаемое в левой части уравнения содержит общий множитель 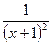 . Вынося его за скобку, получим
. Вынося его за скобку, получим 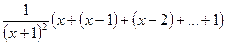 . Выражение в скобках естественно считать суммой
. Выражение в скобках естественно считать суммой 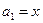 ;
;  ;
; 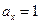 (или
(или 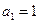 ;
; 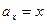 ). Эта сумма равна
). Эта сумма равна 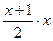 . Таким образом, уравнение принимает вид
. Таким образом, уравнение принимает вид 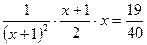 ;
; 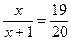 ;
; 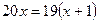 ;
; 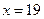 .
.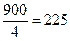 . Вторые числа: 100; 105;…;995. Их количество
. Вторые числа: 100; 105;…;995. Их количество 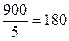 . Трехзначные числа, делящиеся на 20: 100; 120;…; 980. Их количество
. Трехзначные числа, делящиеся на 20: 100; 120;…; 980. Их количество 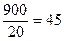 . Заметим, что числа, делящиеся на 20, содержатся и в первой, и во второй группе. Следовательно, количество искомых чисел равно (225-45)+(180-45)=315.
. Заметим, что числа, делящиеся на 20, содержатся и в первой, и во второй группе. Следовательно, количество искомых чисел равно (225-45)+(180-45)=315.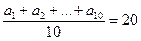 ;
; 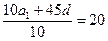 ;
; 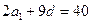 . Так как
. Так как 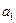 и
и 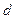 - натуральные, то
- натуральные, то 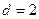 имеем
имеем 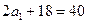 ;
; 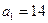 .
. ;
; 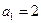 .
.