Текстовые задачи.
При решении текстовых (сюжетных) задач мы пытаемся проиллюстрировать применение математики на практике. При этом важно, чтобы учащийся понимал, что это «применение» включает в себя 3 этапа.
Следует отметить, что все три этапа одинаково значимы и не следует пренебрегать ни одним из них.
7.6. Лодка может проплыть 15 км по течению реки и еще 6 км протии течения за то же время, за какое плот может проплыть 5 км по этой реке. Найдите скорость течения реки, если известно, что собственная скорость лодки 8 км/ч. Решение. Пусть скорость течения реки
Ответ: 2 км/ч.
7.27. На пост мэра города претендовало три кандидата: Андреев, Борисов, Васильев. Во время выборов за Васильева было отдано в 1,5 раза больше голосов, чем за Андреева, а за Борисова – в 4 раза больше, чем за Андреева и Васильева вместе. Сколько процентов избирателей проголосовало за победителя? Решение. Пусть за кандидата А было подано Ответ: 80%. 7.33. Один автомобиль проходит за минуту на 200 м больше, чем другой, поэтому затрачивает на прохождение одного километра на 10 с меньше. Сколько километров в час проходит каждый автомобиль? Решение. Пусть скорость 1 автомобилиста
Решим это уравнение при условии, что
Условию 1000 м/мин или 60 км/ч, а скорость 2 автомобилиста 1200 м/мин или 72 км/ч. Ответ: 60 км/ч, 72 км/ч.
7.47. Одна мельница может смолоть 38 ц пшеницы за 6 ч, а другая – 96 ц за 15 ч, третья – 35 ц за 7 ч. Как распределить 133 т пшеницы между мельницами, чтобы они мололи зерно в течение одного и того же времени? Решение. По условию задачи первая мельница за 1 час может смолоть Пусть каждая мельница работает в течение По условию задачи они должны смолоть 1330 ц пшеницы. Составим уравнение
Значит, на первую мельницу следует отправить
Ответ: 475 ц, 480 ц, 375 ц.
7.55. Цена товара была дважды снижена на одно и то же число процентов. На сколько процентов снижалась цена товара каждый раз, если его первоначальная стоимость 2000р., а окончательная 1850р. Решение. 1 способ. Пусть цена товара дважды снижалась на
Ответ: на 5%. 2 способ.Снижение каждый раз происходило на 5%. Действительно, 5% от 2000р. составляют 100р., а значит, после первого снижения товар стал стоить 1900р. 5% от 1900р. составляют 95р., значит, после второго снижения товар стал стоить 1805р. Очевидно, при снижении стоимости товара больше (меньше), чем на 5% стоимость товара после двух снижений будет меньше (больше) 1805р. Ответ: на 5%.
|

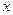 км/ч, тогда скорость лодки по течению
км/ч, тогда скорость лодки по течению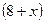 км/ч, а скорость против течения
км/ч, а скорость против течения 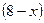 км/ч, причем
км/ч, причем 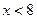 . Значит, на весь путь лодка затрачивает
. Значит, на весь путь лодка затрачивает 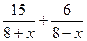 часов, а плот -
часов, а плот - 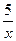 часов. По условию задачи получаем
часов. По условию задачи получаем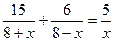 . Решим это уравнение при условии, что
. Решим это уравнение при условии, что 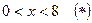 .
.
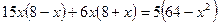
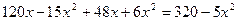
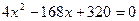
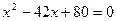
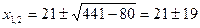 ;
; 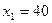 ,
, 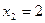 . Неравенству
. Неравенству 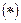 удовлетворяет значение
удовлетворяет значение 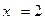 . Значит, скорость течения реки 2 км/ч.
. Значит, скорость течения реки 2 км/ч.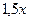 голосов, а за кандидата Б -
голосов, а за кандидата Б - 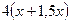 голосов. Значит, всего проголосовало
голосов. Значит, всего проголосовало 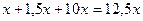 избирателей. Победителем, очевидно, стал кандидат Б, и за него было отдано
избирателей. Победителем, очевидно, стал кандидат Б, и за него было отдано 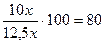 % голосов.
% голосов.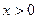 ), тогда скорость 2 – го -
), тогда скорость 2 – го - 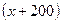 м/мин, значит, 1 автомобилист затрачивает на прохождение 1 км
м/мин, значит, 1 автомобилист затрачивает на прохождение 1 км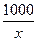 мин, а 2 автомобилист -
мин, а 2 автомобилист - 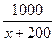 мин. 10 сек составляют
мин. 10 сек составляют 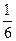 мин. Исходя из условия задачи, получаем
мин. Исходя из условия задачи, получаем 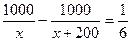 .
.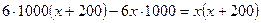
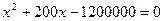
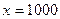 или
или 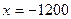 .
.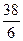 ц пшеницы, вторая -
ц пшеницы, вторая - 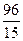 ц, третья -
ц, третья - 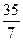 ц.
ц.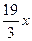 ц, вторая -
ц, вторая - 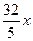 ц, третья -
ц, третья - 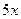 ц.
ц.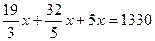
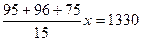
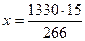
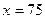 .
.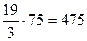 ц, на вторую –
ц, на вторую – ц, на третью -
ц, на третью - 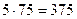 ц.
ц.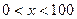 .
. 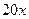 р. Значит, после первого снижения товар стал стоить
р. Значит, после первого снижения товар стал стоить 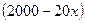 р.
р. 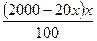 р. Значит, после второго снижения товар стал стоить
р. Значит, после второго снижения товар стал стоить 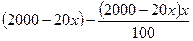 р., что по условию задачи равно 1805р.. Составим уравнение
р., что по условию задачи равно 1805р.. Составим уравнение 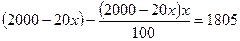 ,
, 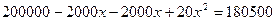
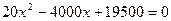
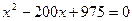
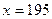 или
или  . Условию (*) удовлетворяет только
. Условию (*) удовлетворяет только 


