Неравенства.
3.3. При каких целых положительных значениях Решение. Сначала найдем все решения данного неравенства Единственным целым положительным числом, удовлетворяющим неравенству, является 1. Ответ: 1.
3.6. Решите систему неравенств Решение. Ответ:
3.12. Найдите область определения выражения Решение. Область определения данного выражения совпадает с множеством решений неравенства Корни:
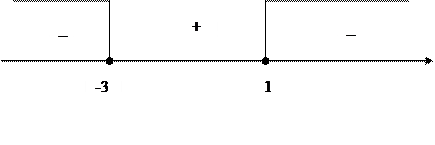
Ответ:
3.14. Какое из чисел больше Решение. 1 способ. Рассмотрим разность Так как знаменатель первой дроби меньше, чем знаменатель второй дроби, то первая дробь больше второй, а значит, разность положительна. Следовательно Ответ: 2 способ.
45 и 48 Так как
Ответ:
3.15. Сравните числа Решение. При сравнении чисел
Ответ:
3.19. Решите неравенство Решение. Так как Ответ:
3.21. Докажите, что дробь
|

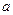 верно неравенство
верно неравенство 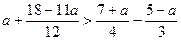 ?
?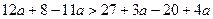 ;
; 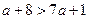 ;
; 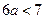 ;
; 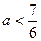 .
.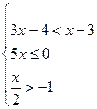 .
.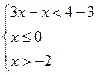 ;
; 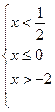 ;
; 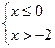 ;
; 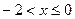 .
. .
.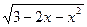 .
.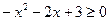 .
.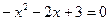 ;
; 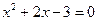 ;
; 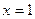 или
или 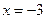 .
.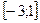 .
.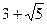 или
или 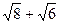 ?
?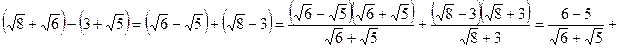
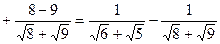 .
.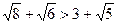 .
.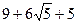 и
и 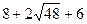
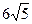 и
и 
 и
и 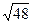
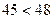 , то
, то 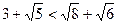 .
. и 12.
и 12.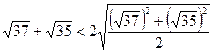 . Так как
. Так как  , то
, то 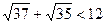 .
.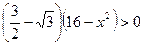 .
.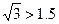 , то
, то  . Тогда данное неравенство равносильно неравенству
. Тогда данное неравенство равносильно неравенству 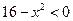 ;
; 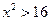 ;
;  .
.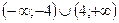 .
. ни при каких значениях
ни при каких значениях  не принимает отрицательные значения.
не принимает отрицательные значения.


