4.4. Постройте график функции 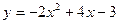 . Укажите наибольшее значение этойфункции.
. Укажите наибольшее значение этойфункции.
Решение. 1) График функции - парабола.
 1. Ветви направлены вниз.
1. Ветви направлены вниз.
2. 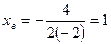 ;
; 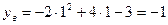 ;
; 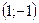 - вершина параболы.
- вершина параболы.
3. 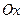 :
: 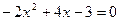 . Так как
. Так как 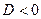 , то график не пересекает ось
, то график не пересекает ось 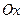 .
.
4. 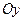 :
:  ;
; 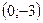 - точка пересечения с осью
- точка пересечения с осью 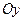 .
.
5. Если 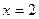 , то
, то 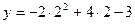 ;
; 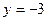 ;
;
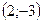 .
.
2) Наибольшее значение функции достигается при 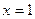 и равно -1.
и равно -1.
4.13. Постройте график функции  . При каких значениях
. При каких значениях  значения функции положительны?
значения функции положительны?
Решение. 1) Так как  , то
, то  .
.
Область определения функции – множество 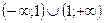 . На указанной области определения данная функция может быть задана формулой
. На указанной области определения данная функция может быть задана формулой 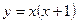 .
.
Построим график функции 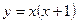 и исключим из него точку с абсциссой
и исключим из него точку с абсциссой 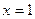 .
.
График функции 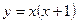 - парабола, ветви которой направлены вверх.
- парабола, ветви которой направлены вверх.
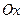 :
: 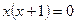 ;
; 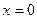 или
или  ;
;  ;
; 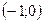 .
.
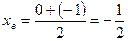 ;
; 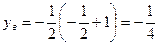 ;
;  .
.
 :
:  .
.
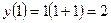 ;
;  ;
;
 ;
;  .
.
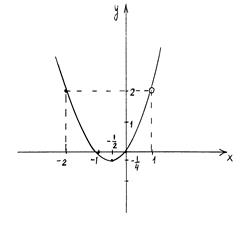
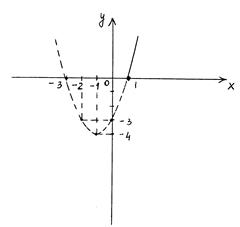
Следовательно, график искомой функции выглядит так, как показано на рисунке.
2) Функция принимает положительные значения на множестве 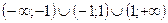 .
.
4.22. Постройте график функции  , где
, где  .
.
При каких значениях  прямая
прямая  имеет с графиком этой функции две общие точки?
имеет с графиком этой функции две общие точки?
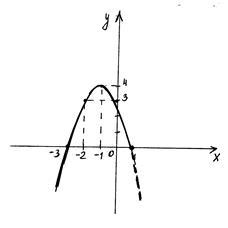 Решение. а) На множестве
Решение. а) На множестве 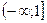 функция задана формулой
функция задана формулой  . Построим график функции
. Построим график функции  и исключим из него точки, абсциссы которых больше 1.
и исключим из него точки, абсциссы которых больше 1.
1. График – парабола, ветви которой направлены вниз.
2. 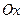 :
: 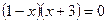 ;
; 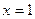 или
или  ;
;  ;
;  .
.
3. 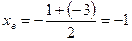 ;
; 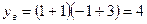 ;
;  .
.
4. 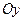 :
:  ;
;  .
.
5.  ;
; 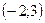 .
.
б) На множестве  функция задана формулой
функция задана формулой  . Построим график функции
. Построим график функции  и оставим только те точки, абсциссы которых больше 1.
и оставим только те точки, абсциссы которых больше 1.
 1 способ.
1 способ.
1. График – парабола, ветви которой направлены вверх.
2. 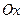 :
: 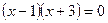 ;
; 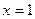 или
или  ;
;  ;
;  .
.
3. 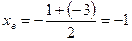 ;
;  ;
;  .
.
4. 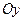 :
:  ;
; 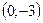 .
.
5.  ;
;  .
.
2 способ. Так как 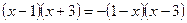 , то график функции
, то график функции  симметричен графику функции
симметричен графику функции  относительно оси
относительно оси 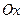 . Воспользовавшись симметрией, построим график функции
. Воспользовавшись симметрией, построим график функции  и оставим только те точки, абсциссы которых больше 1.
и оставим только те точки, абсциссы которых больше 1.

Объединяя оба графика, получим график искомой функции.
в) Прямая  имеет с графиком данной функции две общие точки при
имеет с графиком данной функции две общие точки при 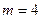 и
и  .
.
4.25. Постройте график функции  .
.
Решение. Так как 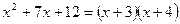 ,
,
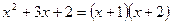 ,
,
 , то
, то  .
.
Область определения функции найдем из условия  , т. е.
, т. е.  и
и 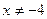 . Значит, множество
. Значит, множество 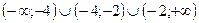 является областью определения.
является областью определения.
На этом множестве функция задается формулой 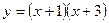 .
.
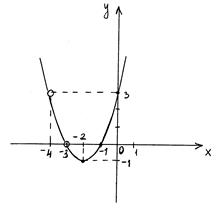 Построим график функции
Построим график функции 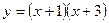 и исключим из него точки с абсциссами
и исключим из него точки с абсциссами  и
и  .
.
График функции 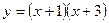 – парабола, ветви которой направлены вверх.
– парабола, ветви которой направлены вверх.
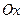 :
: 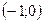 ;
;  .
.
 ;
; 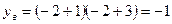 ;
;  .
.
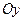 :
:  ;
;  .
.
 ;
; 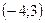 .
.
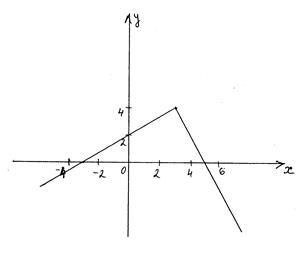 4.28. Задайте аналитически функцию, график которой изображен на рисунке
4.28. Задайте аналитически функцию, график которой изображен на рисунке
Решение. 1 способ. На промежутке  функция линейная, значит, задается формулой
функция линейная, значит, задается формулой 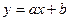 . Так как ее график проходит через точки
. Так как ее график проходит через точки 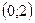 и
и  , то коэффициенты
, то коэффициенты 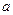 и
и  найдем, решив систему
найдем, решив систему 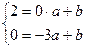 ;
;  ;
; 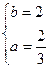 .
.
Следовательно, на промежутке  функция задается формулой
функция задается формулой  .
.
На промежутке  функция также является линейной, значит, тоже задается формулой
функция также является линейной, значит, тоже задается формулой 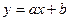 . Так как ее график проходит через точки
. Так как ее график проходит через точки 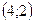 и
и  , то
, то 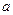 и
и  найдем из системы
найдем из системы 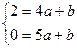 ;
; 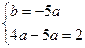 ;
; 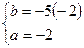 ;
; 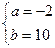 . Следовательно, на промежутке
. Следовательно, на промежутке  функция задается формулой
функция задается формулой 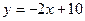 .
.
Таким образом, изображенная на рисунке функция, задается аналитически следующим образом  .
.
2 способ. На каждом из промежутков  и
и  функция является линейной, а значит, задается формулой
функция является линейной, а значит, задается формулой 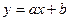 . Точки
. Точки  ,
,  ,
,  лежат на графике функции, значит, коэффициенты
лежат на графике функции, значит, коэффициенты 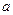 и
и  можно найти следующим образом.
можно найти следующим образом.
1) Если 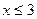 , то
, то  , тогда
, тогда 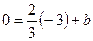 ;
; 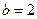 . Следовательно,
. Следовательно,  .
.
2) Если  , то
, то 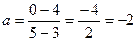 , тогда
, тогда 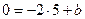 ;
;  . Следовательно,
. Следовательно, 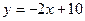 .
.
Итак, формула, задающая функцию, имеет вид  .
.
Ответ:  .
.
4.35. Найдите наибольшее значение функции 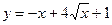 . При каком значении аргумента оно достигается?
. При каком значении аргумента оно достигается?
Решение. 1 способ. Обозначим  . Рассмотрим функцию
. Рассмотрим функцию 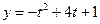 , где
, где 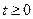 и найдем ее наибольше значение на
и найдем ее наибольше значение на 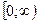 . На
. На 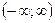 функция
функция 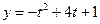 квадратичная, причем коэффициент при
квадратичная, причем коэффициент при 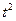 меньше нуля. Значит наибольшее значение она достигает при
меньше нуля. Значит наибольшее значение она достигает при  , т.е. при
, т.е. при  , которое равно
, которое равно  . Так как
. Так как  , то наибольшее значение функции
, то наибольшее значение функции 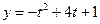 , где
, где 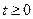 также равно
также равно  , а значит и наибольшее значение функции
, а значит и наибольшее значение функции 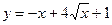 равно
равно  , которое достигается при
, которое достигается при  , т.е. при
, т.е. при  .
.
Ответ: наибольшее значение равно  при
при  .
.
2 способ. Область определения функции 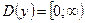 . На этом множестве
. На этом множестве 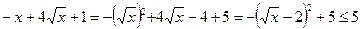 . Равенство достигается при
. Равенство достигается при  , т.е. при
, т.е. при  . Следовательно, наибольшее значение данной функции равно
. Следовательно, наибольшее значение данной функции равно  .
.
Ответ:наибольшее значение равно  при
при  .
.
4.36 Найдите наибольшее значение функции 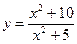 .
.
Решение. 1 способ. Рассмотрим уравнение 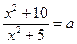 и найдем все значения
и найдем все значения 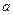 , при которых оно имеет, по крайней мере, одно решение.
, при которых оно имеет, по крайней мере, одно решение.
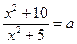 ;
; 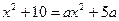 ;
; 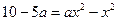 ;
; 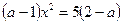 .
.
При  уравнение корней не имеет.
уравнение корней не имеет.
При 
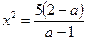 . Последнее уравнение имеет корни при
. Последнее уравнение имеет корни при 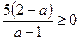 , т.е. при
, т.е. при 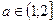 . Значит наибольшее значение функции равно
. Значит наибольшее значение функции равно 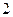 .
.
Ответ: 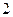 .
.
2 способ. Рассмотрим выражение  .
.
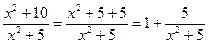 .
.
Дробь  принимает наибольшее значение при наименьшем значении знаменателя, которое равно
принимает наибольшее значение при наименьшем значении знаменателя, которое равно  при
при 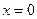 . Следовательно, наибольшее значение дроби
. Следовательно, наибольшее значение дроби  равно
равно  , значит наибольшее значение выражения
, значит наибольшее значение выражения  , а значит, и наибольшее значение функции равно
, а значит, и наибольшее значение функции равно 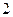 при
при 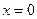 .
.
Ответ: 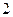 .
.

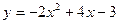 . Укажите наибольшее значение этойфункции.
. Укажите наибольшее значение этойфункции. 1. Ветви направлены вниз.
1. Ветви направлены вниз.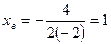 ;
; 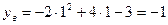 ;
; 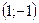 - вершина параболы.
- вершина параболы.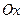 :
: 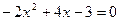 . Так как
. Так как 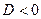 , то график не пересекает ось
, то график не пересекает ось 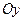 :
:  ;
; 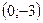 - точка пересечения с осью
- точка пересечения с осью 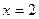 , то
, то 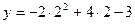 ;
; 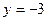 ;
;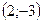 .
.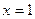 и равно -1.
и равно -1. . При каких значениях
. При каких значениях  значения функции положительны?
значения функции положительны? , то
, то  .
.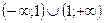 . На указанной области определения данная функция может быть задана формулой
. На указанной области определения данная функция может быть задана формулой 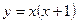 .
.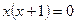 ;
; 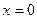 или
или  ;
;  ;
; 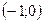 .
.
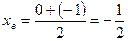 ;
; 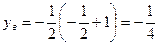 ;
;  .
.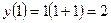 ;
;  ;
; ;
;  .
.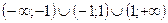 .
. , где
, где  .
. прямая
прямая  имеет с графиком этой функции две общие точки?
имеет с графиком этой функции две общие точки? Решение. а) На множестве
Решение. а) На множестве 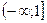 функция задана формулой
функция задана формулой  . Построим график функции
. Построим график функции 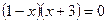 ;
;  ;
;  ;
;  .
.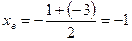 ;
; 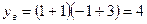 ;
;  .
. ;
;  .
. ;
; 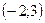 .
. функция задана формулой
функция задана формулой  . Построим график функции
. Построим график функции  1 способ.
1 способ.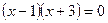 ;
; 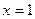 или
или  ;
;  .
. ;
; 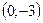 .
. ;
;  .
.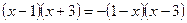 , то график функции
, то график функции 
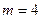 и
и  .
. .
.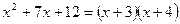 ,
,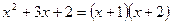 ,
, , то
, то  .
. , т. е.
, т. е.  и
и 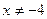 . Значит, множество
. Значит, множество 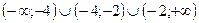 является областью определения.
является областью определения.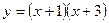 .
. Построим график функции
Построим график функции  и
и  .
. ;
; 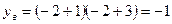 ;
;  .
. ;
;  ;
; 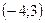 .
. 4.28. Задайте аналитически функцию, график которой изображен на рисунке
4.28. Задайте аналитически функцию, график которой изображен на рисунке функция линейная, значит, задается формулой
функция линейная, значит, задается формулой 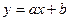 . Так как ее график проходит через точки
. Так как ее график проходит через точки 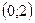 и
и 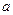 и
и  найдем, решив систему
найдем, решив систему 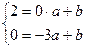 ;
;  ;
; 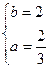 .
. .
. функция также является линейной, значит, тоже задается формулой
функция также является линейной, значит, тоже задается формулой 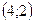 и
и  , то
, то 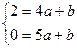 ;
; 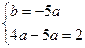 ;
; 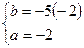 ;
; 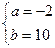 . Следовательно, на промежутке
. Следовательно, на промежутке 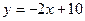 .
. .
. функция является линейной, а значит, задается формулой
функция является линейной, а значит, задается формулой  ,
, 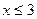 , то
, то  , тогда
, тогда 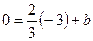 ;
; 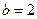 . Следовательно,
. Следовательно,  .
. , то
, то 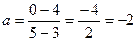 , тогда
, тогда 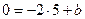 ;
;  . Следовательно,
. Следовательно,  .
.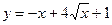 . При каком значении аргумента оно достигается?
. При каком значении аргумента оно достигается? . Рассмотрим функцию
. Рассмотрим функцию 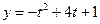 , где
, где 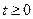 и найдем ее наибольше значение на
и найдем ее наибольше значение на 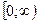 . На
. На 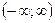 функция
функция 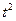 меньше нуля. Значит наибольшее значение она достигает при
меньше нуля. Значит наибольшее значение она достигает при  , т.е. при
, т.е. при  , которое равно
, которое равно  . Так как
. Так как  , то наибольшее значение функции
, то наибольшее значение функции  , а значит и наибольшее значение функции
, а значит и наибольшее значение функции  , т.е. при
, т.е. при  .
.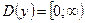 . На этом множестве
. На этом множестве 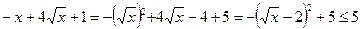 . Равенство достигается при
. Равенство достигается при  , т.е. при
, т.е. при 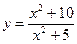 .
.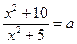 и найдем все значения
и найдем все значения 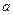 , при которых оно имеет, по крайней мере, одно решение.
, при которых оно имеет, по крайней мере, одно решение.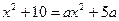 ;
; 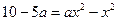 ;
; 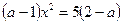 .
. уравнение корней не имеет.
уравнение корней не имеет.
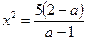 . Последнее уравнение имеет корни при
. Последнее уравнение имеет корни при 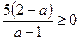 , т.е. при
, т.е. при 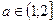 . Значит наибольшее значение функции равно
. Значит наибольшее значение функции равно 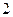 .
. .
.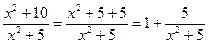 .
. принимает наибольшее значение при наименьшем значении знаменателя, которое равно
принимает наибольшее значение при наименьшем значении знаменателя, которое равно 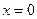 . Следовательно, наибольшее значение дроби
. Следовательно, наибольшее значение дроби  , значит наибольшее значение выражения
, значит наибольшее значение выражения 


