Доказательство.Выражение , являясь неполным квадратом разности, при любых значениях принимает положительные значения. Значит, дробь тоже положительна при всех значениях , ч.т.д.
3.33. Сравните числа Решение. 1 способ.
Так как знаменатель первой дроби меньше, чем знаменатель второй дроби, а их числители равны, то первая дробь больше второй. Следовательно, Ответ: 2 способ. Рассмотрим отношение
Ответ:
3.39. Решите неравенство Решение. Обозначим
Значит
Ответ:
3.45. При каких значениях Решение.
Эта система будет иметь непустое решение тогда и только тогда, когда Ответ: при всех
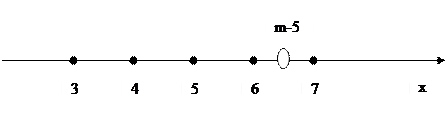
3.46. При каких значениях Решение. Эта система имеет решение тогда и только тогда, когда
Чтобы этому промежутку принадлежали ровно три целых числа, необходимо выполнение следующего условия Ответ: при всех
|
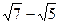и 
.
. 
.
.
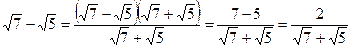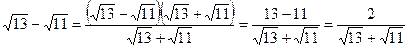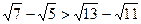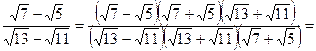
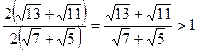. Так как отношение двух положительных чисел больше 1, то числитель больше знаменателя, т.е. 
.
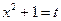, тогда неравенство примет вид 
.
; 
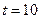или 
.
или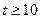 
, т.е.
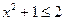или 
;
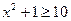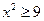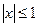или 
;
или 
;
, 
, 
.
.
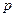система неравенств 
имеет решения?
; 
; 
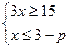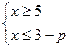
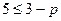, т.е. 
; 
.
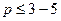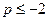система неравенств 
имеет ровно три целых решения?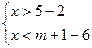
; 
.
. Решением же системы является промежуток 
.
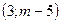, т.е. 
.
.
